 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Графы-2 | Показать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Графы-2 |
|
|
а) 8, 6, 5, 4, 4, 3, 2, 2;
б) 7, 7, 6, 5, 4, 2, 2, 1;
в) 6, 6, 6, 5, 5, 3, 2, 2?
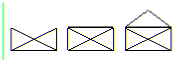
Задача 2: Есть 15 карточек, у каждой из которых на двух сторонах написано по числу. При этом все числа от 1 до 15 написаны по два раза. Доказать, что все карточки можно выложить на стол так, чтобы все числа сверху были различны.Задача 3: Какие из фигур на рисунке можно вычертить, не отрывая карандаша от бумаги и не проводя два раза по одной и той же линии?
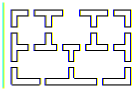
Задача 4:
На рисунке изображен первый этаж дома. Можно ли составить маршрут обхода этого этажа так, чтобы он проходил через каждую дверь ровно один раз?
Задача 5: Гусеница ползает по проволочному каркасу куба. Сможет ли гусеница совершить путешествие по всем двенадцати ребрам, не проползая дважды по одному ребру?
Задача 6: В кружке у любого члена имеется ровно один друг и ровно один враг. Доказать:
а) число членов кружка четно;
б) кружок можно разделить на два нейтральных кружка.
Задача 7: Назовем граф «хлипким», если степень любой его вершины равна 1, 3 или 6. Доказать, что из связного «хлипкого» графа, содержащего 34 ребра, можно выкинуть ребро так, что он перестанет быть связным. Задача 8: В стране Семерка 15 городов, каждый из которых соединен авиалиниями не менее, чем с 7-ю другими. Докажите, что сеть авиалиний Семерки связна. Задача 9: В деревне Вишкиль 9 домов и каждые два из них соединены проволочным телеграфом. Посредством этих телеграфов по деревне распространяются слухи. Сможет ли Петр помешать распространению слуха об исчезновении яблок, перерезав не более семи проводов? Задача 10: Из Москвы выходит 2001 дорога, из деревни Вишкиль – одна, а из всех остальных городов по 1000 дорог. Докажите, что из Москвы по дорогам можно попасть в деревню Вишкиль. Задача 11: В стране из каждого города выходит 100 дорог и от любого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.Задача 12: Из какого минимального числа кусков проволоки с суммарной длиной 12 метров можно спаять каркас куба со стороной 1 метр? Задача 13: Какой максимальной длины можно вырезать кусок проволоки из каркаса куба со стороной 10 см? Задача 14: В стране любые два города соединены или железной дорогой, или авиалинией. Доказать, что один из видов транспорта позволяет добраться из любого города в любой.
Задача 15: Доказать, что из связного графа можно выкинуть вершину со всеми выходящими из нее ребрами, оставив его связным.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Графы-2 | Показать решения |