Задача 1:
Вычислите a)
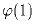
; б)
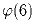
; в)
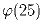
.
Задача 2:
Докажите, что если p – простое число, то
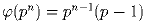
.
Задача 3:
Сколько чисел, меньших 300, делятся а) на 2 и 3; б) на 2, 3 и
5?
Задача 4:
а) Пусть a чисел удовлетворяют какому-то свойству 1, b чисел
удовлетворяют свойству 2, и c чисел удовлетворяют обоим свойствам сразу.
Тогда количество чисел, удовлетворяющих хотя бы одному из этих свойств,
равно a + b – c.
б) Пусть a1 чисел удовлетворяют первому свойству, a2 чисел
удовлетворяют второму свойству, a3 чисел удовлетворяют третьему
свойству, a12 удовлетворяют свойствам 1 и 2, a13
удовлетворяют свойствам 1 и 3, a23 удовлетворяют
свойствам 2 и 3, и a123 удовлетворяют всем трем
свойствам. Тогда количество чисел, удовлетворяющих хотя бы одному из этих
свойств, равно a1a2 + a3 – a12 – a13 – a23 + a123.
Задача 5:
(Формула включения и исключения)
Сформулируйте и докажите аналогичное утверждение для
нахождения количества чисел, удовлетворяющих хотя бы одному из n свойств,
если для каждого набора этих свойств известно количество чисел,
удовлетворяющих одновременно всем свойствам из этого набора.
Задача 6:
а) Пусть n = pq, где p, q – различные простые числа. Докажите, что
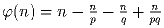
;
б) Пусть n = pqr, где p, q, r –
различные простые числа. Докажите, что 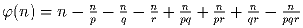 .
.
в) Упростите выражение для 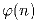 в пунктах а) и б).
в пунктах а) и б).
Задача 7:
Докажите, что в условиях предыдущей задачи а)
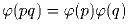
;
б)
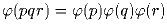
.
Верно ли это, если p, q, r – не простые, а попарно взаимно
простые числа?
Задача 8:
Найдите наименьшее натуральное число, дающее при делении на
2, 3, 5, 7 соответственно остатки 1, 2, 4, 6.
Задача 9:
Пусть даны n попарно взаимно простых чисел m
1,
m
2, …, m
n; n чисел r
1, r
2, …,
r
n таких, что 0 ≤ r
i ≤ m
i – 1 при всех i = 1,2, … ,n
и m = m
1m
2 … m
n.
- Если 0 ≤ N1 ≤ m – 1, 0 ≤ N2 ≤ m – 1,
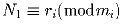 и
и 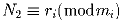 для всех
i = 1,2, … ,n, то N1 = N2.
для всех
i = 1,2, … ,n, то N1 = N2. - Количество различных наборов чисел r1, r2,
…, rn таких, что 0 ≤ ri ≤ mi – 1, равно m.
- (Китайская теорема об остатках) Существует единственное число
N такое, что 0 ≤ N ≤ m – 1
и
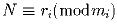 для всех i = 1,2, … ,n.
для всех i = 1,2, … ,n. - N взаимно просто с m Тогда и только тогда, когда N взаимно просто с
mi для всех i = 1,2, … ,n.
- Докажите, что
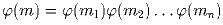 .
.
Задача 10:
Если
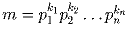
,
то
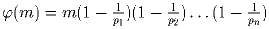
.
Задача 11:
Генерал построил солдат в колонну по 4, но при этом солдат
Иванов остался лишним. Тогда генерал построил солдат в колонну по 5. И снова
Иванов остался лишним. Когда же и в колонне по 6 Иванов оказался лишним,
генерал посулил ему наряд вне очереди, после чего в колонне по 7 Иванов
нашел себе место и никого лишнего не осталось. Сколько солдат могло быть у
генерала?
Задача 12:
Для любых попарно взаимно простых чисел m
1,
m
2, …, m
n и остатков
r
1, r
2, …, r
n
по модулям m
1, m
2, …, m
n найдутся n
последовательных чисел a, a + 1, …, a + n – 1 таких, что
a ≡ r
1 (mod %)%m
1,
a + 1 ≡ r
2 (mod m
2), …, a + n – 1 ≡ r
n (mod %)%m
n.
Задача 13:
Пятнадцать простых чисел образуют арифметическую прогрессию
с разностью d. Докажите, что d > 30000.
Задача 14:
Докажите, что среди а) любых десяти; б) любых шестнадцати
последовательных натуральных чисел найдется число, взаимно простое с
остальными.
Задача 15:
Существует ли в сутках момент, когда расположенные на общей
оси часовая, минутная и секундная стрелки правильно идущих часов образуют
попарно углы в 120?


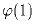 ; б)
; б) 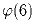 ; в)
; в) 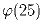 .
Задача 2:
Докажите, что если p – простое число, то
.
Задача 2:
Докажите, что если p – простое число, то 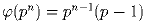 .
Задача 3:
Сколько чисел, меньших 300, делятся а) на 2 и 3; б) на 2, 3 и
5?
Задача 4:
а) Пусть a чисел удовлетворяют какому-то свойству 1, b чисел
удовлетворяют свойству 2, и c чисел удовлетворяют обоим свойствам сразу.
Тогда количество чисел, удовлетворяющих хотя бы одному из этих свойств,
равно a + b – c.
.
Задача 3:
Сколько чисел, меньших 300, делятся а) на 2 и 3; б) на 2, 3 и
5?
Задача 4:
а) Пусть a чисел удовлетворяют какому-то свойству 1, b чисел
удовлетворяют свойству 2, и c чисел удовлетворяют обоим свойствам сразу.
Тогда количество чисел, удовлетворяющих хотя бы одному из этих свойств,
равно a + b – c.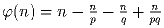 ;
;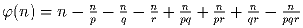 .
.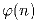 в пунктах а) и б).
в пунктах а) и б).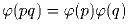 ;
б)
;
б)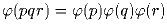 .
Верно ли это, если p, q, r – не простые, а попарно взаимно
простые числа?
Задача 8:
Найдите наименьшее натуральное число, дающее при делении на
2, 3, 5, 7 соответственно остатки 1, 2, 4, 6.
Задача 9:
Пусть даны n попарно взаимно простых чисел m1,
m2, …, mn; n чисел r1, r2, …,
rn таких, что 0 ≤ ri ≤ mi – 1 при всех i = 1,2, … ,n
и m = m1m2 … mn.
.
Верно ли это, если p, q, r – не простые, а попарно взаимно
простые числа?
Задача 8:
Найдите наименьшее натуральное число, дающее при делении на
2, 3, 5, 7 соответственно остатки 1, 2, 4, 6.
Задача 9:
Пусть даны n попарно взаимно простых чисел m1,
m2, …, mn; n чисел r1, r2, …,
rn таких, что 0 ≤ ri ≤ mi – 1 при всех i = 1,2, … ,n
и m = m1m2 … mn.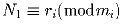 и
и 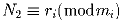 для всех
i = 1,2, … ,n, то N1 = N2.
для всех
i = 1,2, … ,n, то N1 = N2.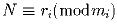 для всех i = 1,2, … ,n.
для всех i = 1,2, … ,n.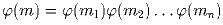 .
.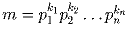 ,
то
,
то 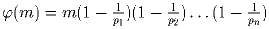 .
Задача 11:
Генерал построил солдат в колонну по 4, но при этом солдат
Иванов остался лишним. Тогда генерал построил солдат в колонну по 5. И снова
Иванов остался лишним. Когда же и в колонне по 6 Иванов оказался лишним,
генерал посулил ему наряд вне очереди, после чего в колонне по 7 Иванов
нашел себе место и никого лишнего не осталось. Сколько солдат могло быть у
генерала?
.
Задача 11:
Генерал построил солдат в колонну по 4, но при этом солдат
Иванов остался лишним. Тогда генерал построил солдат в колонну по 5. И снова
Иванов остался лишним. Когда же и в колонне по 6 Иванов оказался лишним,
генерал посулил ему наряд вне очереди, после чего в колонне по 7 Иванов
нашел себе место и никого лишнего не осталось. Сколько солдат могло быть у
генерала?