 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Комбинаторика | Показать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Комбинаторика |
|
|
Задача 3: Доказать, что Pn = n!. Задача 4: Есть 12 шариков различных цветов и три ящика: красный, синий и зеленый. Сколькими способами можно заполнить ящики шариками (по одному шарику в каждый ящик)?
Задача 5: Доказать, что
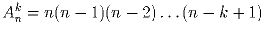 .
Задача 6:
Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать и
переворачивать. Сколько различных бус можно сделать из 16 различных бусинок?
Задача 7:
Сколько различных строк можно получить, переставляя буквы в словах а)
«ВИШКИЛЬ»; б) «МАТЕМАТИТИКА».
Задача 8:
Есть 12 шариков различных цветов. Сколькими способами можно выбрать три
шарика?
Задача 9:
.
Задача 6:
Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать и
переворачивать. Сколько различных бус можно сделать из 16 различных бусинок?
Задача 7:
Сколько различных строк можно получить, переставляя буквы в словах а)
«ВИШКИЛЬ»; б) «МАТЕМАТИТИКА».
Задача 8:
Есть 12 шариков различных цветов. Сколькими способами можно выбрать три
шарика?
Задача 9: а) Остап Бендер достает из мешка k разноцветных слонов и раздает их k детям по слону в руки. Сколькими способами может состояться раздача слонов?
б) А если перед этим ему предстоит выбрать эти k слонов из n разноцветных, находящихся в мешке?
Задача 10: Докажите, что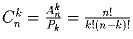 .
Задача 11:
Среди 12 школьников требуется выбрать шесть футболистов. Сколько существует
различных выборов?
Задача 12:
У семиклассника Лени есть 7 книг по математике, а у восьмиклассника Бори –
8 книг. Сколькими способами они могут обменять три книги одного на три книги
другого?
Задача 13:
В кружке «Очумелые ручки» у Ларисы Ивановны занимается 2 девочки и
7 мальчиков. Для участия в конкурсе нужно выбрать четырех человек, среди
которых обязательно должна быть хотя бы одна девочка. Сколькими способами
это можно сделать?
Задача 14:
Сколькими способами можно разбить 10 человек на две баскетбольные команды по
5 человек в каждой?
.
Задача 11:
Среди 12 школьников требуется выбрать шесть футболистов. Сколько существует
различных выборов?
Задача 12:
У семиклассника Лени есть 7 книг по математике, а у восьмиклассника Бори –
8 книг. Сколькими способами они могут обменять три книги одного на три книги
другого?
Задача 13:
В кружке «Очумелые ручки» у Ларисы Ивановны занимается 2 девочки и
7 мальчиков. Для участия в конкурсе нужно выбрать четырех человек, среди
которых обязательно должна быть хотя бы одна девочка. Сколькими способами
это можно сделать?
Задача 14:
Сколькими способами можно разбить 10 человек на две баскетбольные команды по
5 человек в каждой?Задача 15: На окружности отмечены 5 красных, 7 желтых и 9 зеленых точек. Сколько существует треугольников с вершинами в этих точках, у которых все вершины а) зеленые; б) одноцветные; в) все разноцветные; г) не все одноцветные? Задача 16: У скольких 10-значных чисел все цифры различны? Задача 17: Сколькими способами можно расставить k ладей на доске N × N так, чтобы они не били друг друга? Задача 18: Среди 12 школьников требуется выбрать дежурных на ближайшие шесть дней – на каждый день по дежурному. Сколько существует различных выборов? Задача 19:
Вычислите или упростите: а) 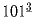 ; б)
; б) 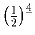 ; в)
; в) 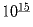 ;
г)
;
г) 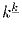 , где k – натурально.
, где k – натурально.
Задача 20:
Для проведения вступительной олимпиады преподаватели разбивают 70 школьников следующим образом: список в алфавитном порядке разбивается на 4 части, первая идет в первую аудиторию, вторая – во вторую и т. д. При этом в каждую аудиторию отправляется хотя бы один школьник. Сколькими способами можно произвести распределение?
Задача 21: Сколько решений имеет уравнение x + y + z = 2000 а) в натуральных числах; б) в целых неотрицательных числах? Задача 22: Преподаватели снова делят 70 школьников на 4 аудитории, но в этот раз без учета алфавитного порядка. Найдите число способов. Задача 23: Хромая ладья ходит на 1 клетку вправо или на 1 клетку вверх. Занумеруем столбцы слева направо, а строки снизу вверх числами 0, 1, 2, 3. Найдите количество путей, ведущих из левой нижней клетки в клетку на пересечении m-го столбца и n-ной строки. Задача 24: Сколько решений в нечетных натуральных числах имеет уравнение x + y + z + t = 2000? Задача 25: Сколько есть решений уравнения x + y + z = 100 в натуральных числах от 1 до 60? Задача 26: Сколькими способами можно расставить числа 1, 2, , 20 в строку так, чтобы каждое число, кроме единицы, было больше по крайней мере одного из своих соседей?| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Комбинаторика | Показать решения |