Задача 1:
В таблице N × N, заполненной числами, все строки различны (две строки
называются различными, если они отличаются хотя бы в одном элементе).
Докажите, что из таблицы можно вычеркнуть один столбец так, что в оставшейся
таблице опять все строки будут различны.
Задача 2:
На плоскости расположено несколько непрозрачных кругов и точка. Докажите,
что из этой точки некоторый круг виден полностью (то есть, что другие круги
его не загораживают его даже частично).
Задача 3:
Трое велосипедистов ездят с различными постоянными скоростями по круглому
велотреку. У них есть фляжка, которая обязательно передается от одного к
другому при встрече или обгоне (ситуаций, когда все трое оказываются
одновременно в одном месте, не случается). Может ли оказаться, что как бы
долго они не ездили, к одному из них фляжка так и не попадет?
Задача 4:
На какое количество нулей может оканчиваться число вида 1
n + 2
n + 3
n + 4
n при натуральных n? (Найдите все возможные ответы)
Задача 5:
На сторонах AB и AC правильного треугольника ABC отмечены точки
D и E соответственно
так, что AD = CE, и в треугольнике ADE проведена медиана
AM. Докажите, что BE = 2AM.
Задача 6:
Брат-старшеклассник спросил сестренку-младшеклассницу: «Сколько дней тебе
было ровно втрое меньше полных лет, чем мне?»
– 3 дня, – ответила
сестренка.
– А ровно в 4 раза?
– 4 дня.
– А ровно в 6 раз?
Тут сестренка
задумалась. Она помнила, что такие дни были, но вот сколько…Помогите
ей найти ответ.
Задача 7:
Для натуральных чисел a, b, c известно, что
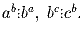
Докажите, что
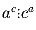
.
Задача 8:
В противоположных углах клетчатой доске 7 × 8 ставятся черная и белая
ладьи, остальные поля заполняются серыми пешками. Двое играющих ходят по
очереди каждый своей ладьей. Каждым ходом игрок обязан что-нибудь съесть –
пешку или ладью противника. Проигрывает тот, кто не сможет сделать хода. Кто
из игроков может выигрывать независимо от игры противника?


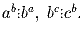 Докажите, что
Докажите, что 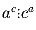 .
Задача 8:
В противоположных углах клетчатой доске 7 × 8 ставятся черная и белая
ладьи, остальные поля заполняются серыми пешками. Двое играющих ходят по
очереди каждый своей ладьей. Каждым ходом игрок обязан что-нибудь съесть –
пешку или ладью противника. Проигрывает тот, кто не сможет сделать хода. Кто
из игроков может выигрывать независимо от игры противника?
.
Задача 8:
В противоположных углах клетчатой доске 7 × 8 ставятся черная и белая
ладьи, остальные поля заполняются серыми пешками. Двое играющих ходят по
очереди каждый своей ладьей. Каждым ходом игрок обязан что-нибудь съесть –
пешку или ладью противника. Проигрывает тот, кто не сможет сделать хода. Кто
из игроков может выигрывать независимо от игры противника?