 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Площади и отношения. Ослабление условий (профи) | Показать решения |
|
|
| Материалы Кировской ЛМШ, 2000 г, 7 класс. Площади и отношения. Ослабление условий (профи) |
|
|
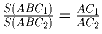 .
.б) Точка A лежит на отрезке C1C2.
Докажите, что 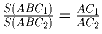 .
.
в) В треугольниках A1B1C1 и A2B2C2
∠ A1 = ∠ A2.
Докажите, что 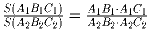 .
.
г) В треугольниках A1B1C1 и A2B2C2
∠ A1 + ∠ A2 = 180°. Докажите, что
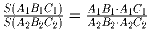 .
.
б) Две параллельные прямые высекают на сторонах угла с вершиной O отрезки
A1A2 и B1B2. Докажите, что
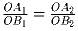 .
.
в) (Теорема Фалеса) Три параллельные прямые пересекают стороны угла в точках 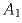 ,
B1, C1 и A2, B2, C2
соответственно. Докажите, что
,
B1, C1 и A2, B2, C2
соответственно. Докажите, что 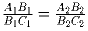 .
.
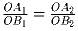 . Докажите,
что прямые параллельны.
Задача 5:
На сторонах угла с вершиной O отмечены точки A1,
A2 и B1, B2. При этом
. Докажите,
что прямые параллельны.
Задача 5:
На сторонах угла с вершиной O отмечены точки A1,
A2 и B1, B2. При этом 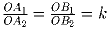 . Найдите отношение
. Найдите отношение
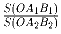 .
Задача 6:
На стороне AB треугольника ABC сидит жук Кирюша.
Он начинает
ползти параллельно стороне BC до стороны AC,
затем параллельно стороне AB до
стороны BC, затем параллельно стороне AC до стороны AB,
и так далее. Докажите, что
через несколько шагов Кирюша вернется в исходную точку, и найдите сколько
шагов ему на это потребуется (ответ может зависеть от исходного положения
жука на AB).
.
Задача 6:
На стороне AB треугольника ABC сидит жук Кирюша.
Он начинает
ползти параллельно стороне BC до стороны AC,
затем параллельно стороне AB до
стороны BC, затем параллельно стороне AC до стороны AB,
и так далее. Докажите, что
через несколько шагов Кирюша вернется в исходную точку, и найдите сколько
шагов ему на это потребуется (ответ может зависеть от исходного положения
жука на AB).Задача 7: Даны точка P и две пары параллельных прямых (a\|a′, b\|b′, но a и b – не параллельны). Проведите через точку P прямую так, чтобы обе пары параллельных прямых отсекали на ней равные отрезки. Задача 8: Даны две пересекающиеся прямые. Найдите ГМТ, расположенных вдвое ближе к первой чем ко второй прямой. Задача 9: а) Найдите геометрическое место четвертых вершин квадратов, у которых три вершины лежат на сторонах данного угла.
б) Впишите квадрат в данный треугольник так, чтобы две вершины квадрата попали на данную сторону.
Задача 10: Даны угол ABC и точка M внутри него. Постройте окружность, касающуюся сторон угла и проходящую через точку M. Задача 11: В треугольнике ABC провели медиану AM, а затем – биссектрисы BK и BL полученных треугольников AMB и AMC соответственно. Докажите, что отрезки KL и BC параллельны.
Задача 12: Даны две параллельные прямые и отрезок на одной из них. С помощью одной линейки разделите этот отрезок а) на две равные части; б)* на три равные части.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2000 г, 7 класс >> Площади и отношения. Ослабление условий (профи) | Показать решения |