Задача 1:
Фигура «верблюд» ходит по доске 10 × 10 на три клетки по вертикали и
одну по горизонтали, или на три по горизонтали и одну по вертикали. Можно ли
пройти «верблюдом» с какого-то исходного поля на соседнее с ним по стороне?
Задача 2:
По кругу расставлены числа 12,7,23,45,13,5. За один ход можно прибавить или
отнять одно и то же число от двух стоящих рядом чисел. Можно ли за несколько
ходов получить числа 7,13,4,2,5,12?
Задача 3:
В каждой клетке на доске 7 × 7 сидит жук. По команде все жуки
переползают на соседние по стороне клетки. Доказать, что после этого
какая-то клетка останется пустой.
Задача 4:
Дети и преподаватели 7-го класса стоят на линейке в виде квадрата 9 × 9, и у каждого из них пьет кровь комар. В момент подъема флага все комары
взлетают и садятся на соседнего по диагонали человека. Докажите, что после
такого массового перелета по крайней мере девятерых страдальцев никто не
будет кусать.
Задача 5:
Докажите, что доску 8 × 8 нельзя замостить 15 фигурками 1 × 4 и
одной фигуркой из четырех клеток в форме буквы «Г».
Задача 6:
ЛМыШонок ест куб сыра 3 × 3 × 3, съедая за один присест один
кубик 1 × 1 × 1. После того, как кубик съеден, ЛМыШонок
переходит к соседнему с ним по грани кубику. Может ли этот зверь съесть весь
сыр без центрального кубика.
Задача 7:
В трех вершинах квадрата находятся 3 кузнечика, играющие в чехарду. При этом
если кузнечик A прыгает через кузнечика B,
то после прыжка он оказывается на
том же расстоянии от него, но по другую сторону и на той же прямой. Может ли
после нескольких прыжков один из кузнечиков попасть в четвертую вершину
квадрата?
Задача 8:
Дно прямоугольной коробки выложено плитками 2 × 2 и 1 × 4.
Плитки высыпали из коробки и потеряли одну плитку 2 × 2. Вместо нее
достали плитку 1 × 4. Докажите, что выложить дно коробки плитками
теперь не удастся.
Задача 9:
Докажите, что квадрат 6 × 6 нельзя разрезать на 11 прямоугольников
1 × 3 и один уголок из трех клеток.
Задача 10:
На доске 8 × 8 в левом нижнем углу в виде квадрата 3 × 3 лежат
9 фишек. За ход разрешается какой-нибудь одной фишке перепрыгнуть через
какую-нибудь другую (не обязательно соседнюю) фишку на клетку, симметричную
первой фишке относительно второй (если эта клетка свободна). Можно ли после
нескольких таких ходов собрать все фишки в квадрате 3 × 3 а) в левом
верхнем углу доски; б) в правом верхнем углу доски?
Задача 11:
Из доски 248 × 198 вырезали 1999 крестиков из пяти клеток. Докажите,
что из оставшейся части можно вырезать еще один такой крестик.
Задача 12:
Как раскрасить лист клетчатой бумаги в 5 цветов так, чтобы внутри любой
фигуры типа А (см. рисунок) клетки были окрашены во все 5 цветов, а внутри
любой фигуры типа В – не все?
Задача 13:
Нарисуйте на плоскости а) 6; б) 11 одинаковых неперекрывающихся квадратов
так, чтобы их нельзя было правильно раскрасить в 3 цвета. (Правильной
называется раскраска, при которой любые две фигуры, имеющие общую часть
границы, окрашены в разные цвета.)
Задача 14:
Докажите, что доску размером 10 × 10 клеток нельзя разрезать на
фигурки в форме буквы «Т», состоящей из 4-х клеток.
Задача 15:
Клетчатый прямоугольник 2000 × 2001 разрезали на фигуры трех видов:

,
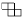
,
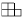
.
Какое при этом могло получится наименьшее количество фигур вида
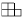 Задача 16:
Задача 16:
Докажите, что если вершины выпуклого n-угольника лежат в узлах клетчатой
бумаги, а внутри и на его сторонах других узлов нет, то n < 5.


 ,
, 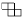 ,
, 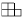 .
Какое при этом могло получится наименьшее количество фигур вида
.
Какое при этом могло получится наименьшее количество фигур вида 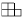 Задача 16:
Докажите, что если вершины выпуклого n-угольника лежат в узлах клетчатой
бумаги, а внутри и на его сторонах других узлов нет, то n < 5.
Задача 16:
Докажите, что если вершины выпуклого n-угольника лежат в узлах клетчатой
бумаги, а внутри и на его сторонах других узлов нет, то n < 5.