Задача 1:
Существует ли тупоугольный треугольник, который можно разрезать на
остроугольные треугольники?
Задача 2:
Найдите все решения в натуральных числах уравнения
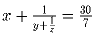
.
Задача 3:
Клетки доски 10 × 10 пронумерованы от 1 до 100 по порядку: на первой
горизонтали от 1 до 10 слева направо, на второй – от 11 до 20 и т. д. На
доску выставлены 10 ладей, не бьющих друг друга. Докажите, что сумма чисел
под ними не зависит от расстановки ладей.
Задача 4:
Что больше: 200! или 100²ºº?
Задача 5:
Стороны нескольких прямоугольников параллельны осям координат. Известно, что
любые два из них имеют общую точку. Докажите. что все они имеют общую точку.
Задача 6:
Найдите внутри квадрата ABCD все точки X такие, что
AX + CX = BX + DX.
Задача 7:
После удачного налета атаман Рустам взял себе одиннадцатую часть всех
захваченных пленниц, а остальных распределил между членами шайки согласно их
заслугам. Косой, которому досталось меньше всех пленниц, затеял драку с
атаманом и был побежден в честном бою. Труп его достался шакалам, а
пленницы – атаману, после чего у атамана оказалась одна восьмая всех пленниц.
Доказать, что после драки у атамана осталось не больше 25 разбойников.
Задача 8:
Имеется кучка из 262 камней. Оля, Катя и Лариса играют в следующую игру: за
один ход каждая может взять 1, 4 или 10 камней. Первой ходит Оля, второй –
Катя и последней – Лариса. Потом опять Оля, и т. д. Выигрывает та, которая
берет последний камень. Кто из них может выигрывать независимо от игры
соперниц?


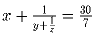 .
Задача 3:
Клетки доски 10 × 10 пронумерованы от 1 до 100 по порядку: на первой
горизонтали от 1 до 10 слева направо, на второй – от 11 до 20 и т. д. На
доску выставлены 10 ладей, не бьющих друг друга. Докажите, что сумма чисел
под ними не зависит от расстановки ладей.
Задача 4:
Что больше: 200! или 100²ºº?
Задача 5:
Стороны нескольких прямоугольников параллельны осям координат. Известно, что
любые два из них имеют общую точку. Докажите. что все они имеют общую точку.
Задача 6:
Найдите внутри квадрата ABCD все точки X такие, что
AX + CX = BX + DX.
Задача 7:
После удачного налета атаман Рустам взял себе одиннадцатую часть всех
захваченных пленниц, а остальных распределил между членами шайки согласно их
заслугам. Косой, которому досталось меньше всех пленниц, затеял драку с
атаманом и был побежден в честном бою. Труп его достался шакалам, а
пленницы – атаману, после чего у атамана оказалась одна восьмая всех пленниц.
Доказать, что после драки у атамана осталось не больше 25 разбойников.
Задача 8:
Имеется кучка из 262 камней. Оля, Катя и Лариса играют в следующую игру: за
один ход каждая может взять 1, 4 или 10 камней. Первой ходит Оля, второй –
Катя и последней – Лариса. Потом опять Оля, и т. д. Выигрывает та, которая
берет последний камень. Кто из них может выигрывать независимо от игры
соперниц?
.
Задача 3:
Клетки доски 10 × 10 пронумерованы от 1 до 100 по порядку: на первой
горизонтали от 1 до 10 слева направо, на второй – от 11 до 20 и т. д. На
доску выставлены 10 ладей, не бьющих друг друга. Докажите, что сумма чисел
под ними не зависит от расстановки ладей.
Задача 4:
Что больше: 200! или 100²ºº?
Задача 5:
Стороны нескольких прямоугольников параллельны осям координат. Известно, что
любые два из них имеют общую точку. Докажите. что все они имеют общую точку.
Задача 6:
Найдите внутри квадрата ABCD все точки X такие, что
AX + CX = BX + DX.
Задача 7:
После удачного налета атаман Рустам взял себе одиннадцатую часть всех
захваченных пленниц, а остальных распределил между членами шайки согласно их
заслугам. Косой, которому досталось меньше всех пленниц, затеял драку с
атаманом и был побежден в честном бою. Труп его достался шакалам, а
пленницы – атаману, после чего у атамана оказалась одна восьмая всех пленниц.
Доказать, что после драки у атамана осталось не больше 25 разбойников.
Задача 8:
Имеется кучка из 262 камней. Оля, Катя и Лариса играют в следующую игру: за
один ход каждая может взять 1, 4 или 10 камней. Первой ходит Оля, второй –
Катя и последней – Лариса. Потом опять Оля, и т. д. Выигрывает та, которая
берет последний камень. Кто из них может выигрывать независимо от игры
соперниц?