Задача 1: От прямоугольника 324 × 141 отрезают квадраты со стороной 141 до тех пор, пока это возможно. Затем от полученного прямоугольника отрезают квадраты, у которых сторона равна меньшей из сторон прямоугольника и т.д. Сколько квадратов в конце концов получится и какого они будут размера?

Задача 2: То же самое делают с прямоугольником 770 × 315. Чему равна длина стороны самого маленького квадрата?

Задача 3: На доске написаны числа a и b. Разрешается заменять одно из чисел на сумму или разность имеющихся чисел. Какое минимальное натуральное число можно получить такими операциями, если

а) a = 100, b = 151;

б) a = 100, b = 255;

в) a = 7n + 3, b = 9n + 4?

Задача 4: Три автомата печатают на карточках пары натуральных чисел. Каждый автомат, прочитав некоторую карточку, выдаёт новую. Прочитав карточку с парой (m,n), первый автомат выдаёт пару (m – n,n), второй – пару (m + n,n), а третий – пару (n,m). Можно ли, используя эти автоматы, получить:

a) из карточки (12,21) карточку (19,97);

b) из карточки (19,97) карточку (12,21);

c) из карточки (13,31) карточку (19,97)?

Задача 5: Докажите, что все общие делители чисел a и b, являются также общими делителями чисел b и a – kb (k – произвольное целое число).

Задача 6: Пусть r – остаток от деления a на b. Докажите, что

а) все общие делители чисел a и b, являются также общими делителями чисел b и r.

б) все общие делители чисел b и r, являются также общими делителями чисел a и b.

в) Докажите, что  НОД (a,b) =  НОД (b,r).

Задача 7: [Алгоритм Евклида] Используя результат предыдущей задачи, придумайте алгоритм для вычисления  НОД (a,b).

Задача 8: Докажите, что

а)  НОД (2a,2b) = 2 НОД (a,b);

б)  НОД (2a,2b + 1) =  НОД (a,2b + 1);

в)  НОД (2a + 1,2b + 1) =  НОД (a – b,2b + 1).

Задача 9: Используя результат предыдущей задачи, придумайте ещё один алгоритм вычисления  НОД (a,b).

Задача 10: Не разлагая числа на простые множители, вычислите  НОД (861,637) и  НОД (2001,22012000).

Задача 11: Докажите, что дробь 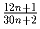несократима ни при каком натуральном n.

Задача 12: Докажите, что  НОД (3n + 2,10n + 23) может быть равен только 1, 7 или 49.

Задача 13: Найти пару чисел, не больших 1000, для которых алгоритм Евклида заканчивает работу (получает два равных числа) только через 14 шагов.

Задача 14: Найти НОД числа, десятичная запись которого состоит из 100 единиц, и числа, десятичная запись которого состоит из 60 единиц.

Задача 15: Найти  НОД (2¹ºº – 1,2⁶⁰ – 1).