 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Индукция-1. Знакомство с ММИ | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Индукция-1. Знакомство с ММИ |
|
|
 ).
Решение:
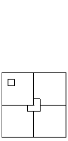
Указание: Переход: разбиваем квадрат на четыре квадрата
2n – 1 × 2n – 1 и вырезаем из каждой недырявой части
угловую клетку так, чтобы вырезанные клетки образовали уголок.
).
Решение:
Указание: Переход: разбиваем квадрат на четыре квадрата
2n – 1 × 2n – 1 и вырезаем из каждой недырявой части
угловую клетку так, чтобы вырезанные клетки образовали уголок.
Задача 2: Докажите, что любую сумму, начиная с 8 тугриков, можно выплатить купюрами по 3 тугрика и 5 тугриков. Решение: Указание: Переход: меняем купюру в 5 тугриков на две купюры по 3 тугрика. Если же пятитугриковых купюр нет – меняем три купюры по 3 тугрика на две купюры по 5 тугриков… Задача 3: Приведите пример натурального числа, которое равно сумме а) трёх своих различных делителей; б) ста своих различных делителей. Решение: а) 6; б) 297 • 6. Переход: n → 2n (в список суммируемых делителей добавляется число n). Задача 4: Докажите, что при каждом натуральном n, начиная с 3, существует выпуклый n-угольник, имеющий ровно три острых угла. Решение: Указание: Переход: стороны AB и BC, образуюшие тупой угол, заменяем на отрезок A′C′ (A′ ∈ AB; C′ ∈ BC). Вновь образованные углы AA′C′ и CC′A – внешние углы треугольника A′BC′, а значит «тупее» угла B… Задача 5: У бородатого многоугольника во внешнюю сторону растет щетина. Его пересекает несколько прямых общего положения, на каждой из которых с одной из сторон растут волосы. В результате многоугольник оказался разбитым на некоторое число частей. Докажите, что хотя бы одна из частей окажется волосатой снаружи. Решение: Указание: Проводим прямые одну за другой. Если очередная прямая пересекает волосатую снаружи часть, то часть, оказавшаяся с неволосатой стороны – также волосатая снаружи… Задача 6: [Игра «Ханойская башня»] Имеется пирамида с n кольцами возрастающих размеров (внизу – самое большое) и еще два пустых стержня той же высоты. Разрешается перекладывать верхнее кольцо с одного стержня на другой, но при этом запрещается класть большее кольцо на меньшее. Докажите, что
а) можно переложить все кольца с первого стержня на один из пустых стержней;
б) это можно сделать не более, чем за 2n – 1 перекладываний.
Решение: Указание: Пусть мы умеем переность пирамиду высоты k – 1.
1. Перенести k – 1 кольцо на пустой стержень
2. Перенести k-е кольцо на другой пустой стержень.
3. Переносим k – 1 кольцо на тот же стержень
Задача 7: Плоскость поделена на области несколькими прямыми. Докажите, что эти области можно раскрасить в два цвета так, чтобы любые две соседние области были раскрашены в различные цвета. (Соседними считаются области, имеющие общий участок границы.)Задача 8: В прямоугольнике 3 × n (3 строки, n столбцов) расставлены фишки трёх цветов по n штук каждого цвета. Докажите, что переставляя фишки в строчках, можно сделать так, чтобы в каждом столбце были фишки всех трёх цветов.
Задача 9: Плоскость поделена на области несколькими прямыми и окружностями. Докажите, что эти области можно раскрасить в два цвета так, чтобы любые две соседние области были раскрашены в различные цвета. (Соседними считаются области, имеющие общий участок границы.)
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Индукция-1. Знакомство с ММИ | Убрать решения |