 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Разнобой-1 | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Разнобой-1 |
|
|
Задача 2: Можно ли 16 жирафов попарно разного роста расставить в шеренгу так, что какие бы 11 жирафов не вышли из шеренги, оставшиеся 5 не будут стоять по росту? Решение: Да. Пусть жирафы пронумерованы по росту (1 – самый низкий, 16 – самый высокий). Расставим жирафов в таком порядке: 13, 14, 15, 16, 9, 10, 11, 12, 5, 6, 7, 8, 1, 2, 3, 4.
Задача 3: Все клетки доски 10 × 10 покрашены в белый цвет. Владик и Юра по очереди (начинает Владик) перекрашивают по одной белой клетке в черный цвет. Проигрывает тот, после чьего хода на доске не останется двух соседних по стороне белых клеток. Кто выигрывает при правильной игре? Решение: Юра. Он разбивает все клетки на пары (парой объявляются клетки из одной «доминошки», доска разбивается на доминошки произвольно) и каждый раз ходит в клетку, парную к той, куда сходил Владик.
Задача 4: Десятичная запись числа 5 • A состоит из 1000 пятерок и 1000 шестерок. Найдите сумму цифр числа A. Решение: 4000. Представим 5 • A в виде суммы числа 55 … 5 (2000 пятерок) и числа, в котором на некоторых 1000 местах стоят единички, а на остальных – нули. Тогда 10 • A равно сумме числа 11 … 10 и числа, в котором на некоторых 1000 местах стоят двойки, а на остальных – нули. Сумма цифр этого числа равна 2000 + 2000 = 4000, а у числа A сумма цифр точно такая же, как у числа 10 • A.
Задача 5: На доске выписали все возможные девятизначные числа, которые можно получить из цифры 9, записывая каждый раз за последней цифрой либо её же, либо цифру, меньшую её на 1 (например, так можно получить число 998766543). Сколько раз встречается цифра 3 среди последних цифр этих чисел? Решение:
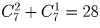 . Мы должны выбрать те две цифры, которые
в этом числе будут повторяться.
. Мы должны выбрать те две цифры, которые
в этом числе будут повторяться. 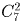 соответствует выбору
пары различных цифр, а
соответствует выбору
пары различных цифр, а 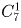 – выбору тройки одинаковых цифр.
– выбору тройки одинаковых цифр. Задача 6: Дан угол, величина которого 82 . Пользуясь только циркулем и линейкой, построить угол в 33 . Решение: Указание: Если дополнить 82 до прямого угла, то получится 8. Если провести биссектрису угла 82, то получится 41. Наконец, 41 – 8 = 33.
Задача 7: Есть 10 монет, среди них ровно две фальшивые. Детектор R7 за одну операцию исследует три монеты и указывает на одну из них. Известно, что детектор не может указать на настоящую монету, если среди тестируемых монет есть хотя бы одна фальшивая. Как за шесть тестов выявить обе фальшивые монеты?
Задача 8: Серединный перпендикуляр к стороне BC треугольника ABC пересекает сторону AB в точке D, а продолжение за точку A стороны AC — в точке E. Докажите, что AD < AE.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Разнобой-1 | Убрать решения |