Задача 1:
Какие две цифры нужно приписать справа к числу 1983, чтобы
получилось число, делящееся на 83?
Задача 2:
Найдите все двузначные числа, обладающие следующим свойством: если
вставить между цифрами числа произвольное ненулевое
количество семёрок, то
полученное число делится нацело на 13.
Задача 3:
На поле брани встретились армии Толстых и Тонких по 1000 человек
в каждой. Сначала каждый
Толстый выстрелил в одного из Тонких. Затем каждый уцелевший Тонкий
выстрелил в одного из Толстых. Наконец, каждый уцелевший Толстый ещё
раз выстрелил в одного из Тонких. После этого у каждой армии кончились
патроны. Докажите, что в живых осталось не менее 500 солдат.
Задача 4:
Решите ребус
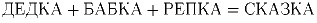
.
Задача 5:
Через точку плоскости проведены 3 прямые, разбивающие плоскость
на 6 углов. Известно, что один из образовавшихся углов не превосходит
полусуммы наибольшего и наименьшего угла. Докажите,
что этот угол не превосходит 60.
Задача 6:
Если класс из 30 человек рассадить в зале кинотеатра, то в
любом случае хотя бы в одном ряду окажется не менее двух
одноклассников. Если то же самое проделать с классом из 26
человек, то по крайней мере три ряда окажутся пустыми. Сколько
рядов в зале?
Задача 7:
На складе стеклотары могут храниться банки из-под консервированных овощей
по 0.5 л, 0.7 л и 1 л. Сейчас на складе имеется 2500 банок общей
вместимостью 1998 л. Докажите, что на складе есть хотя бы одна поллитровая
банка.
Задача 8:
Все натуральные числа поделены на хорошие и плохие.
Известно, что если число A хорошее, то и число A + 6 тоже хорошее,
а если число B плохое, то и число B + 15 тоже плохое. Может ли
среди первых 2000 чисел быть ровно 1000 хороших?


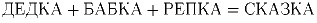 .
.