 |
 |
|
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Разнобой-5 | Убрать решения |
|
|
| Разное. Материалы Кировской ЛМШ, 2001 г, 7 класс. Разнобой-5 |
|
|
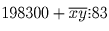 . Первое
слагаемое при делении на 83 дает остаток 13. Значит,
. Первое
слагаемое при делении на 83 дает остаток 13. Значит,
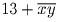 делится на 83, из чего заключаем, что
делится на 83, из чего заключаем, что
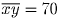 , то есть нужно приписать цифры 7 и 0.
Задача 2:
Найдите все двузначные числа, обладающие следующим свойством: если
вставить между цифрами числа произвольное ненулевое
количество семёрок, то
полученное число делится нацело на 13.
Решение:
Пусть
, то есть нужно приписать цифры 7 и 0.
Задача 2:
Найдите все двузначные числа, обладающие следующим свойством: если
вставить между цифрами числа произвольное ненулевое
количество семёрок, то
полученное число делится нацело на 13.
Решение:
Пусть 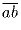 — двузначное число, обладающее требуемым
свойством. Тогда числа
— двузначное число, обладающее требуемым
свойством. Тогда числа 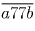 и
и 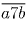 , а
следовательно, и их разность, равная 100(9a + 7) делятся на 13. Так
как 100 и 13 взаимно просты, на 13 делится число 9a + 7, откуда
перебором всех возможных случаев получаем, что a может равняться только 5.
Из делимости на 13 числа
, а
следовательно, и их разность, равная 100(9a + 7) делятся на 13. Так
как 100 и 13 взаимно просты, на 13 делится число 9a + 7, откуда
перебором всех возможных случаев получаем, что a может равняться только 5.
Из делимости на 13 числа 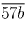 находим, что b = 2,
то есть 52 – единственно возможный
вариант.
находим, что b = 2,
то есть 52 – единственно возможный
вариант.
Убеждаемся, что все числа вида  делятся на 13. Это
немедленно следует из
равенства:
делятся на 13. Это
немедленно следует из
равенства: 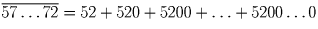 .
.
Задача 3: На поле брани встретились армии Толстых и Тонких по 1000 человек в каждой. Сначала каждый Толстый выстрелил в одного из Тонких. Затем каждый уцелевший Тонкий выстрелил в одного из Толстых. Наконец, каждый уцелевший Толстый ещё раз выстрелил в одного из Тонких. После этого у каждой армии кончились патроны. Докажите, что в живых осталось не менее 500 солдат. Решение: Пусть Тонкие своим единственным залпом убили n Толстых. Тогда вторым залпом Толстые убьют не более 1000 – n Тонких, поэтому за два последних залпа погибнет не более 1000 солдат с той и другой стороны.
Пусть после первого залпа Толстых в живых осталось x Тонких. Возможны два случая:
1) x ≤ 500. Тогда после залпа Тонких у Толстых останется в живых не менее 1000 – x солдат, что не меньше 500, и утверждение в этом случае доказано.
2) x > 500. Тогда после первого залпа Толстых у двух армий в сумме более 1500 живых солдат. Как показано выше, за два последних залпа не может погибнуть более 1000 человек, что и завершает доказательство.
Задача 4: Решите ребус
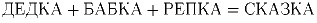 .
.Задача 5: Через точку плоскости проведены 3 прямые, разбивающие плоскость на 6 углов. Известно, что один из образовавшихся углов не превосходит полусуммы наибольшего и наименьшего угла. Докажите, что этот угол не превосходит 60. Решение: Обозначим три подряд идущих угла через α , β и γ . Оставшиеся три угла также будут соответственно равны α , β и γ , как вертикальные. Без ограничения общности, пусть α ≤ β ≤ γ . Тогда
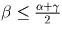 , откуда α + γ ≥ 2 β .
Но углы α , β и γ составляют развёрнутый угол, поэтому
π = α + β + γ ≥ 3 β , откуда и следует утверждение
задачи.
, откуда α + γ ≥ 2 β .
Но углы α , β и γ составляют развёрнутый угол, поэтому
π = α + β + γ ≥ 3 β , откуда и следует утверждение
задачи.Задача 6: Если класс из 30 человек рассадить в зале кинотеатра, то в любом случае хотя бы в одном ряду окажется не менее двух одноклассников. Если то же самое проделать с классом из 26 человек, то по крайней мере три ряда окажутся пустыми. Сколько рядов в зале? Решение: Первое условие означает, что в зале не более 29 рядов. Действительно, если бы количество рядов было не меньше 30, то, очевидно, класс из 30 человек можно было бы рассадить не более чем по одному на каждый ряд.
Второе условие означает, что количество рядов в зале не менее 29. Действительно, если количество рядов не больше 28, то сажая учеников класса из 26 человек по очереди на пустые ряды, получим, что либо в какой-то момент все ряды будут заняты, либо все 26 учеников будут сидеть по одному на 26 рядах, и в этом случае останутся свободными не более двух рядов.
Значит, в кинотеатре 29 рядов. Очевидно, что в этом случае оба условия задачи выполнены.
Задача 7: На складе стеклотары могут храниться банки из-под консервированных овощей по 0.5 л, 0.7 л и 1 л. Сейчас на складе имеется 2500 банок общей вместимостью 1998 л. Докажите, что на складе есть хотя бы одна поллитровая банка.Задача 8: Все натуральные числа поделены на хорошие и плохие. Известно, что если число A хорошее, то и число A + 6 тоже хорошее, а если число B плохое, то и число B + 15 тоже плохое. Может ли среди первых 2000 чисел быть ровно 1000 хороших? Решение: Докажем, что числа C и C + 3 являются одновременно либо хорошими, либо плохими при любом значении C. Предположим для этого, что число C — хорошее, а C + 3 — плохое. Тогда с одной стороны, число C + 18 = (C + 3) + 15 должно быть хорошим, а с другой стороны, это же число C + 18 = ((C + 6) + 6) + 6 должно быть плохим. Если же предположить, что число C — плохое, а C + 3 — хорошее, то число C + 15 = ((C + 3) + 6) + 6 должно быть одновременно и плохим и хорошим. Полученное в обоих случаях противоречие доказывает, что числа C и C + 3 всегда принадлежат одному классу. Из этого следует, что любой класс вычетов по модулю 3 является либо целиком хорошим, либо целиком плохим.
Среди первых 2000 чисел каждый такой класс содержит 666 или 667 чисел. Любой класс содержит меньше 1000 чисел, а любые два класса — больше 1000 чисел. Поэтому ровно 1000 хороших чисел быть не может.
| Задачная база >> Разное >> Материалы Кировской ЛМШ, 2001 г, 7 класс >> Разнобой-5 | Убрать решения |