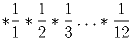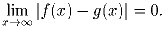Задача 1:
На доске написано следующее выражение:
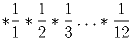
- Докажите, что невозможно заменить звёздочки на + 1 и – 1 так, чтобы
значение выражения стало равным 0.
- Какое наименьшее количество дробей надо убрать, чтобы стало
возможным сделать значение оставшегося выражения равным 0 путём
замены звёздочек на + 1 и – 1.
Задача 2:
Несколько круглых дисков одинакового диаметра лежат на столе,
некоторые из них могут касаться других, но никакие два диска не
перекрываются. Места для других дисков того же диаметра на столе нет.
Докажите, что диски покрывают более четверти поверхности стола.
Задача 3: Даны n попарно взаимно простых натуральных чисел, каждое из
которых больше 1, но меньше чем (2n – 1)². Докажите, что
по крайней мере одно из этих чисел – простое.
Задача 4: В треугольнике ABC угол A не прямой.
Точки F и G
выбраны на AB и CA, соответственно, так, что
BG и CF являются высотами треугольника ABC. Окружность
ρ проходит через точки
A, F, G. Касательных к ρ в точках F и G
пересекаются в точке I. Докажите, что I лежит на BC.
Задача 5: Пусть f(x) и g(x) – периодические функции. Известно, что
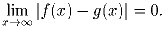
Докажите, что f(x) = g(x) для всех x.