 |
 |
|
| Задачная база >> Заочные и дистанционные олимпиады >> Internet Mathematics Olympiad >> 2001 >> Июнь | Показать решения |
|
|
| Internet Mathematics Olympiad. 2001. Июнь |
|
|
Докажите, что для произвольных положительных x1,x2,x3,x4,x5 выполняется следующее неравенство: (x1 + x2 + x3 + x4 + x5)² ≥ 4(x1x2 + x2x3 + x3x4 + x4x5 + x5x1).
Задача 2: ABC – треугольник на координатной плоскости, вершины которого имеют целые координаты. Предположим, что только одна точка с целыми координатами находится внутри ABC (но нет никаких ограничений на точки на сторонах). Докажите, что площадь треугольника ABC не превосходит 9/2. Задача 3:
Докажите, что любое натуральное число n может быть представено в виде
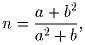
Пусть U = 1,2, … ,n, π = (i1,i2, … ,in) – перестановка чисел 1,2, … ,n, а S – подмножество U. Мы говорим, что π разбивает S, если S ≠ ik,ik + 1, … ,im для всех k и m. Например, π = (1,3,5,4,2) разбивает 1,2,3, но не 3,4,5.
Пусть 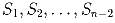 – семейство подмножеств U таких, что 2 ≤ |Si| ≤ n – 1 для i = 1,2, … ,n – 2. Докажите, что существует
перестановка чисел 1,2, … ,n, которая разбивает все
подмножества
– семейство подмножеств U таких, что 2 ≤ |Si| ≤ n – 1 для i = 1,2, … ,n – 2. Докажите, что существует
перестановка чисел 1,2, … ,n, которая разбивает все
подмножества 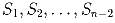 .
.
Задача 5:
На вечеринке у каждых двух человек есть ровно один общий друг. Докажите, что существует такой человек, который является другом всех остальных.
| Задачная база >> Заочные и дистанционные олимпиады >> Internet Mathematics Olympiad >> 2001 >> Июнь | Показать решения |