 |
 |
|
| Задачная база >> Заочные и дистанционные олимпиады >> Internet Mathematics Olympiad >> 2001 >> Март | Показать решения |
|
|
| Internet Mathematics Olympiad. 2001. Март |
|
|
Решите уравнение
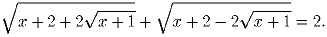
Города A и B стоят на одной реке, причём город B расположен ниже по течению, чем город A. В 9 утра плот отправляется из A в B и одновременно лодка отправляется из B в A. Лодка и плот встретились через 5 часов. После прибытия в A лодка повернула обратно и прибыла в B одновременно с плотом. Могло ли жто случиться раньше 9 вечера того же дня?
Задача 3:
В классе n ≥ 3 учеников. Каждые двое из них – друзья или враги. Каждый день один ученик начинает новую жизнь, в результате чего все его враги становятся его друзьями, а его друзья – его врагами. Известно, что каждые три человека могут стать друзьями после нескольких таких изменений. Докажите, что все ученики могут стать друзьями.
Задача 4:
Пусть точка D лежит внутри или на стороне треугольника ABC, а P – произвольная точка. Докажите, что PA + PB + PC + PD ≥ DA + DB + DC, причём равенство достигается в том и только том случае, когда P = D.
Задача 5:Докажите, что уравнение a² + b² + c² + 2 = abc имеет бесконечно много решений.
| Задачная база >> Заочные и дистанционные олимпиады >> Internet Mathematics Olympiad >> 2001 >> Март | Показать решения |