Задача 1: Ожерелье пани Моники состоит из разноцветных бусинок. Моника любит выкладывать свое ожерелье на стол в форме правильного многоугольника (так, чтобы в каждой вершине находилась бусинка, а число бусинок на каждой стороне было одним и тем же). Это ей удается, когда число сторон равно 3, 4, 5 или 6, причем всегда в вершинах оказываются бусинки разных цветов. Найдите наименьшее возможное число различных по цвету бусинок.

Задача 2: Петр выписал на доску 77 приведенных квадратных трехчленов и проверил, что ни один из них не имеет (действительных) корней. Докажите, что и сумма этих трехчленов также не имеет корней.

Задача 3: Репдиджитом в некоторой системе счисления называется число, запись которого в этой системе счисления состоит из одинаковых цифр (более одной). Например, десятичное число 2001 является репдиджитом в системе счисления с основанием 666. Проверьте это и найдите основания еще трех систем счисления, в которых 2001 является репдиджитом.

Задача 4: Решите в неотрицательных числах систему:

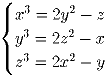
Задача 5:

В пространстве дан (косоугольный) параллелепипед единичного объема. Докажите, что расстояние между какими-то его двумя вершинами не меньше .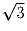

Задача 6:

Какое наибольшее число шаров могут попарно (каждый с каждым) касаться друг друга (внешним образом)?
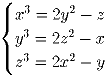
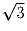