Задача 1: Автобусный билет имеет шестизначный номер (от 000001 до 999999).
Билет называется счастливым, если сумма первых трех цифр номера равна
сумме трех его последних цифр. Докажите, что количество счастливых
билетов не больше 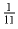 от общего числа билетов.
от общего числа билетов.
Задача 2:
Может ли выпуклый многогранник иметь только семиугольные грани?
Задача 3:
Докажите, что n
7 – 36n делится на 7 при любом натуральном n.
Задача 4:
Заседания научной конференции будут проходить в трех секциях:
алгебры, геометрии и комбинаторики, а официальными языками
конференции объявлены русский, английский и китайский. Известно, что
каждый участник конференции собирается сделать два доклада на разных
секциях и владеет ровно двумя из этих языков. Организаторы хотят
провести конференцию за два дня и так составить ее расписание, чтобы
в течение дня никто из участников не переходил из одной секции в
другую, но все присутствующие могли бы понять каждый доклад. Как
можно составить такое расписание?
Задача 5:
Найдите все натуральные x , для которых
((xx + 1)x + xx)((xx + 1)x – 1 + xx(x + 1)) = 2001
Задача 6:
Из прямоугольного листа бумаги вырезали пять пятиугольников так, что
оставшаяся часть образует выпуклый многоугольник. Сколько сторон он может
иметь?


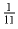 от общего числа билетов.
от общего числа билетов.