Задача 1: x1,x2, … ,xn – положительные числа,
S = x1 + x2 + • s + xn. Докажите, что
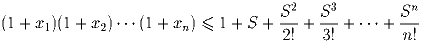
Задача 2: Докажите, что уравнение
6(6a² + 3b² + c²) = 5n²
не имеет целочисленных решений, отличных от a = b = c = n = 0.
Задача 3: A1,A2,A3 – три точки на плоскости, не лежащие на одной
прямой. Для удобства, положим A4 = A1,A5 = A2. При
n = 1,2,3,4 Bn – середина отрезка AnAn + 1, а Cn – середина
AnBn. При n = 1,2,3 прямые AnCn + 1 и BnAn + 2 пересекаются в
точке Dn, а прямые AnBn + 1 и CnAn + 2 – в точке En.
Найдите отношение площадей треугольников D1D2D3 и E1E2E3.
Задача 4: S – множество, состоящее из m пар (a,b) натуральных чисел,
удовлетворяющих условию 1 ≤ a < b ≤ n. Докажите, что существует по
крайней мере 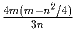 троек чисел (a,b,c) таких, что
(a,b), (a,c) и (b,c) принадлежат S.
троек чисел (a,b,c) таких, что
(a,b), (a,c) и (b,c) принадлежат S.
Задача 5: Найдите все функции f, определенные на множестве вещественных
чисел, такие, что
- [(1)] f(x) строго возрастает,
- [(2)] f(x) + f – 1(x) = 2x для всех вещественных x,
где через f
– 1 обозначена функция обратная к f.


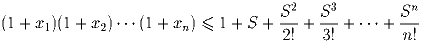
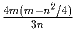 троек чисел (a,b,c) таких, что
(a,b), (a,c) и (b,c) принадлежат S.
троек чисел (a,b,c) таких, что
(a,b), (a,c) и (b,c) принадлежат S.