Задача 1: Даны неотрицательные целые числа a₁, a₂,…,a_n. Пусть

([x] – целая часть x). Докажите, что a₁! • a₂! •  … a_n! ≥ a!ⁿ. Найдите все a₁, a₂,…,a_n такие, что a₁! • a₂! •  … a_n! = a!ⁿ.

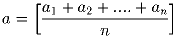
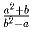Задача 2: Найдите все пары натуральных чисел a и b такие, что и 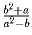 – целые числа.

Задача 3: На сторонах AC и AB равностороннего треугольника ABC взяты точки P и Q соответственно так, что углы APB и CQA – острые. S – центр описанной окружности треугольника ABP, R – центр описанной окружности треугольника AQC. Известно, что TR = RS = ST. Найдите все возможные величины углов PBC и QCB.

Задача 4: Пусть x,y,z > 0 и

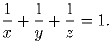
Докажите, что

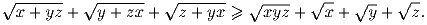
Задача 5: Найдите все 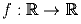такие, что

(i) f(x) = 0 для конечного числа значений x (возможно, f(x) ≠ 0 для всех x)

(ii) f(x⁴ + y) = x³*f(x) + f(f(y)).