 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 4 олимпиада | Показать решения |
|
|
| Международные соревнования. Международная МО. 4 олимпиада |
|
|
Найдите наименьшее натуральное число, последняя цифра которого – 6, и которое увеличивается в 4 раза от переноса этой цифры в начало.
Задача 2:Найдите все вещественные x для которых 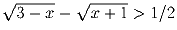 .
.
По периметру граней ABCD и B′C′CB куба ABCDA′B′C′D′ с одинаковой скоростью двигаются точки X и Y. Точка X начинает двигаться из A по направлению к B и одновременно с ней точка Y начинает двигаться из B′ к C′. Найдите геометрическое место середин отрезков XY.
Задача 4:Найдите все вещественные решения уравнения cos ²x + cos ²2x + cos ²3x = 1.
Задача 5:Даны три различные точки A,B,C лежащие на окружности K. Постройте точку D на K такую, чтобы четырехугольник ABCD был бы описанным.
Задача 6:Докажите, что расстояние между центром окружности, вписанной
в равнобедренный треугольник и центром описанной вокруг него окружности
равно 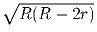 , где R и r – радиусы описанной и вписанной
окружностей соответственно.
, где R и r – радиусы описанной и вписанной
окружностей соответственно.
Докажите, что тетраэдр является правильным тогда и только тогда, когда существует пять сфер, каждая из которых касается всех шести ребер тетраэдра или их продолжений.
| Задачная база >> Международные соревнования >> Международная МО >> 4 олимпиада | Показать решения |