 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 21 олимпиада | Показать решения |
|
|
| Международные соревнования. Международная МО. 21 олимпиада |
|
|
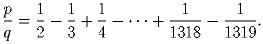
Доказать, что на плоскости существует неподвижная точка P такая, что расстояния от точек M1 и M2 до P равны в течение всего времени движения.
Задача 4: [США] Дана плоскость α , точка P на этой плоскости и точка Q вне плоскости α . Найти все точки R в плоскости α , для которых отношение (|QP| + |PR|)/|QR| максимально. Задача 5: [Израиль] Найти все вещественные числа a, для которых существуют вещественные неотрицательные числа x1, x2, x3, x4, x5, удовлетворяющие соотношениям: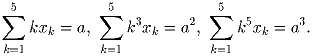
Задача 6: [ФРГ] Пусть A и E – две противоположные вершины правильного восьмиугольника. В вершине A находится кенгуру. Из любой вершины восьмиугольника, кроме вершины E, кенгуру может прыгнуть в любую из двух соседних вершин. Попав в вершину E, кенгуру останавливается и остается там. Пусть an – количество способов, которыми кенгуру может попасть из A в E ровно за n прыжков. Доказать, что
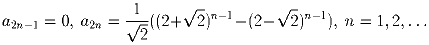
1) P0 = A,
2) Pn = E,
3) для любого i, 0 ≤ i ≤ n – 1, Pi ≠ E,
4) для любого i, 0 ≤ i ≤ n – 1, Pi и Pi + 1 – соседние вершины многоугольника.
| Задачная база >> Международные соревнования >> Международная МО >> 21 олимпиада | Показать решения |