 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 25 олимпиада | Убрать решения |
|
|
| Международные соревнования. Международная МО. 25 олимпиада |
|
|
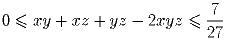
1) число ab(a + b) не делится на 7
2) (a + b)7 – a7 – b7 делится на 77.
Ответ обосновать.
Задача 3: [Румыния] На плоскости даны две различные точки O и A. Для каждой точки X этой плоскости, отличной от точки O, обозначим через a(X) величину угла AOX, выраженную в радианах (0 ≤ a(x) < 2 π ), где угол a(x) отсчитывается против часовой стрелки от луча OA, а через C(X) – окружность с центром O и радиусом OX + a(X)/OX.Пусть задан конечный набор цветов, и каждая точка плоскости окрашена в один из них. Докажите, что существует точка Y такая, что a(Y) > 0 и на окружности C(Y) имеется хотя бы одна точка того же цвета, что и точка Y.
Задача 4: [Румыния] Пусть в выпуклом четырехугольнике ABCD прямая CD касается окружности с диаметром AB. Докажите, что прямая AB касается окружности с диаметром CD тогда и только тогда, когда прямые BC и AD параллельны. Задача 5: [Монголия] Пусть d – сумма всех диагоналей, а p – периметр плоского выпуклого n-угольника (n > 3). Докажите, что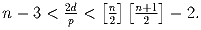 Задача 6:
[Польша] Пусть a, b, c, d – нечетные целые числа,
удовлетворяющие следующим условиям:
Задача 6:
[Польша] Пусть a, b, c, d – нечетные целые числа,
удовлетворяющие следующим условиям:1) 0 < a < b < c < d;
2) ad = bc;
3) a + d = 2k, b + c = 2m для некоторых целых чисел m и k. Докажите, что a = 1.
| Задачная база >> Международные соревнования >> Международная МО >> 25 олимпиада | Убрать решения |