Задача 1: [Люксембург] На плоскости даны две окружности с общим центром, радиусы которых соответственно равны r и R, r < R. Пусть P – фиксированная точка на маленькой окружности и B – переменная точка на большой окружности. Прямая BP пересекает второй раз большую окружность в точке C. Перпендикуляр l к прямой BC, проходящий через точку P, пересекает второй раз маленькую окружность в точке A (в случае, когда l – касательная к окружности, считаем, что A = P).

1) Найдите множество значений выражения BC² + CA² + AB².

2) Найдите множество точек, являющихся серединами отрезков AB.

Задача 2: [Чехословакия] Пусть n – натуральное число и A₁, A₂, …, A_2n + 1 – подмножества некоторого множества B. Предположим, что

a) каждое множество A_i (i = 1,2, … ,2n + 1) содержит ровно 2n элементов;

b) каждое множество A_i ∩ A_j(1 ≤ i < j ≤ 2n + 1) содержит ровно один элемент;

c) любой элемент множества B принадлежит не менее чем двум из множеств A_i (i = 1,2, … ,2n + 1).

Для каких значений n можно поставить в соответствие каждому элементу множества B одно из чисел 0 или 1 так, чтобы каждое из множеств A₁, A₂, …, A_2n + 1 содержала бы ровно n элементов, соответствующих числу нуль?

Задача 3: [Англия] Функция f определена на множестве натуральных чисел и удовлетворяет следующим условиям: f(1) = 1, f(3) = 3, f(2n) = f(n), f(4n + 1) = 2f(2n + 1) – f(n), f(4n + 3) = 3f(2n + 1) = 2f(n). Найдите число всех таких значений n, 1 ≤ n ≤ 1988, для которых f(n) = n.

Задача 4: [Ирландия] Докажите, что множество решений неравенства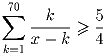

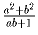является объединением непересекающихся промежутков, сумма длин которых равна 1988.

Задача 5: [Греция] Пусть AD – высота в прямоугольном треугольнике ABC, угол A меньше 90. Прямая, проходящая через центры окружностей, вписанных в треугольники ABD и ACD, пересекает стороны AB и AC соответственно в точках K и L. Докажите, что S_ABC ≥ 2 • S_AKL.

Задача 6: [ФРГ] Пусть a и b – такие целые положительные числа, что a² + b² делится на ab + 1 без остатка. Докажите, что является квадратом целого числа.