Задача 1: [СССР] Дан треугольник ABC. Пусть A′, B′, C′ – точки пересечения биссектрис углов CAB, ABC, BCA со сторонами BC, CA, AB соответственно и I – центр вписанной окружности. Докажите, что

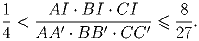
Задача 2: [Румыния] Пусть n – целое число, n > 6 и a₁, a₂, …, a_k – это все натуральные числа, которые меньше n и взаимно просты с n. Докажите, что если a₂ – a₁ = a₃ – a₂ =  …  = a_k – a_k – 1 > 0, то n – или простое число, или натуральная степень числа 2.

Задача 3: [Китай] Пусть S = 1,2, … ,280. Найдите наименьшее натуральное число n такое, что любое n-элементное подмножество множества S содержит 5 попарно взаимно простых чисел.

Задача 4: [США] Дан связный граф G с k ребрами. Докажите, что можно занумеровать ребра всеми числами 1, 2, …, k так, что для каждой вершины графа, которая соединена ребрами не менее чем с двумя другими вершинами, набор чисел, которыми помечены эти ребра, не имеет общего делителя, большего 1.

Задача 5: [Франция] Пусть P – внутренняя точка треугольника ABC. Докажите, что хотя бы один из углов PAB, PBC, PCA не больше 30.

Задача 6: [Нидерланды] Бесконечная последовательность действительных чисел x₀,x₁,x₂, …  называется ограниченной, если существует постоянная C такая, что |x_i| ≤ C для каждого i ≥ 0.

Дано действительное число a > 1. Постройте ограниченную бесконечную последовательность x₀,x₁,x₂, …  такую, что неравенство |x_i – x_j| • |i – j|^a ≥ 1 выполнено для каждой пары различных чисел i и j.