 |
 |
|
| Задачная база >> Международные соревнования >> Международная МО >> 34 олимпиада | Показать решения |
|
|
| Международные соревнования. Международная МО. 34 олимпиада |
|
|
Пусть f(x) = xn + 5xn – 1 + 3, где n > 1 – целое число. Доказать, что f(x) не может быть представлен в виде произведения двух многочленов, каждый из которых степени не меньше 1 и все коэффициенты которых – целые числа.
Задача 2:Дан остроугольный треугольник ABC и точка D внутри него, такая что ∠ ADB = ∠ ACB + 90 и AC • BD = AD • BC.
а) Вычислить значение отношения 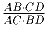 ;
;
б) Доказать, что касательные, проведенные в точке C к окружности, описанной около треугольников ACD и BCD, перпендикулярны.
Задача 3:На бесконечной шахматной доске ведется игра. В начале n² фишек занимают поле n × n, по одной фишке в каждой клетке. Ход заключается в том, что какая-то фишка перепрыгивает в горизонтальном или вертикальном направлении через одну соседнюю занятую клетку на свободную клетку за ней. При этом фишка, через которую перепрыгнули, снимается с доски. Найти все n, для которых можно оставить на доске всего одну фишку.
Задача 4:Для трех точек P,Q,R на плоскости через m(PQR) обозначим наименьшую из длин высот треугольника PQR. Пусть на плоскости даны точки A,B,C,D . Доказать m(ABC) ≤ m(ABD) + m(ADC) + m(DBC).
Задача 5:Существует ли функция 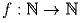 такая, что
такая, что
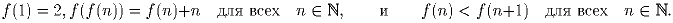
Пусть n > 1 – целое число. По окружности расположено n ламп L0, … ,Ln – 1. Каждая лампа может быть в состоянии «включена» или «выключена». Последовательность шагов S0,S1, … ,Si, … определена следующим образом. Шаг Sj влияет только на состояние лампы Lj (и не влияет на состояние остальных ламп) так что, если Lj – 1 включена, то Sj изменяет состояние лампы Lj (то есть, если Lj была включена, то станет выключена и наоборот). Если Lj – 1 выключена, то Sj ничего не меняет. Лампы пронумерованы по модулю n (т.е. Ln = L0 и т.д.)
Первоначально все лампы включены. Доказать, что
а) Существует натуральное M(n) такое, что после M(n) все лампы будут включены.
б) Если n – число вида 2k, то после n² – 1 шагов все лампы будут включены.
в) Если n – число вида 2k + 1, то после n² – n + 1 шагов все лампы будут включены.
| Задачная база >> Международные соревнования >> Международная МО >> 34 олимпиада | Показать решения |