Задача 1:

Найдите все конечные множества S состоящие не менее чем из трех точек плоскости, симметричные относительно серединных перпендикуляров отрезков с концами из S.

Задача 2:

Найдите наименьшее C такое, что при фиксированном n

для любых неотрицательных x₁,x₂, … ,x_n и для этого значения C определите, когда достигается равенство.

Задача 3:

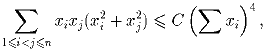
Найдите минимальное количество клеток, которые можно покрасить на доске 2n × 2n так, чтобы у любая клетка (в том числе покрашенная) граничила бы по стороне с покрашенной клеткой.

Задача 4:

Найдите все пары чисел n,p для которых p простое, n ≤ 2p и (p – 1)ⁿ + 1 делится на n^p – 1.

Задача 5:

Окружности  Γ ₁ и  Γ ₂ лежат внутри окружности  Γ  и касаются ее в точках M и N соответственно, притом, центр окружности  Γ ₂ лежит на  Γ ₁. Продолжение общей хорды окружностей  Γ ₁ и  Γ ₂ пересекает  Γ  в точках A и B. Прямые MA и MB повторно пересекают  Γ ₁ в точках C и D. Докажите, что прямая CD касается  Γ ₂.

Задача 6:

Найдите все функции 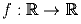такие, что f(x – f(y)) = f(f(y)) + xf(y) + f(x) – 1.