Задача 1:
Окружности Γ
1 и Γ
2 пересекаются в точках M и N.
Прямая l – общая касательная к Γ
1 и Γ
2 такая, что
M расположена к l ближе, чем N. Прямая l касается Γ
1
в точке A, а Γ
2 – в точке B. Прямая, проходящая через
M параллельно l, пересекает вторично окружность Γ
1 в
точке C, а окружность Γ
2 – в точке D. Прямые CA и
DB пересекаются в точке E, прямые AN и CD – в точке P,
прямые BN и CD – в точке Q. Докажите, что EP = EQ.
Задача 2:
Положительные числа a, b, c таковы, что abc = 1. Докажите, что
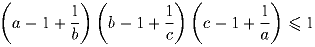
Задача 3: Дано натуральное число n > 2. Сначала на горизонтальной прямой сидят
n блох, не все в одной точке. Для положительного действительного
числа λ определим прыжок следующим образом: выбираются
две блохи, сидящие в произвольных точках A и B, причём A левее
B, и блоха, сидящая в A, прыгает в точку C, расположенную на
данной прямой справа от B, такую, что 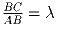 .
Определите все значения λ такие, что для любой точки M на
этой прямой и для любого начального расположения n блох существует
конечная последовательность прыжков, после которой все блохи окажутся
справа от точки M.
.
Определите все значения λ такие, что для любой точки M на
этой прямой и для любого начального расположения n блох существует
конечная последовательность прыжков, после которой все блохи окажутся
справа от точки M.
Задача 4: У фокусника 100 карточек, занумерованных числами от 1 до 100. Он
раскладывает все карточки в три ящика: красный, белый и синий так,
чтобы в каждом ящике лежала хотя бы одна карточка. Один из зрителей
выбирает два из трёх ящиков, вынимает из них по одной карточке и
объявляет сумму номеров вынутых карточек. Зная эту сумму, фокусник
определяет тот ящик, из которого карточка не вынималась. Сколькими
различными способами можно разложить карточки по ящикам так, чтобы
этот фокус всегда удавался? (Способы, при которых хотя бы одна
карточка попадает в разные ящики, считаются различными.)
Задача 5:
Существует ли натуральное число n такое, что n имеет ровно 2000
различных простых делителей, и 2
n + 1 делится на n.
Задача 6:
Пусть AH
1, BH
2, CH
3 – высоты остроугольного треугольника
ABC. Окружность, вписанная в треугольник ABC, касается сторон
BC, CA, AB в точках T
1, T
2, T
3 соответственно. Прямые
l
1, l
2, l
3 являются образами прямых H
2H
3, H
3H
1,
H
1H
2 при симметрии относительно прямых T
2T
3, T
3T
1,
T
1T
2 соответственно. Докажите, что прямые l
1, l
2, l
3
образуют треугольник с вершинами на окружности, вписанной в
треугольник ABC.


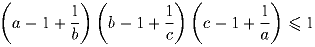
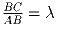 .
Определите все значения λ такие, что для любой точки M на
этой прямой и для любого начального расположения n блох существует
конечная последовательность прыжков, после которой все блохи окажутся
справа от точки M.
.
Определите все значения λ такие, что для любой точки M на
этой прямой и для любого начального расположения n блох существует
конечная последовательность прыжков, после которой все блохи окажутся
справа от точки M.