Задача 1:

Пусть O – центр описанной окружности остроугольного треугольника ABC, AP – высота. Докажите, что если  ∠ BCA ≥  ∠ ABC + 30, то  ∠ CAB +  ∠ COP < 90.

Решение:

Решение 1.

Пусть  α  =  ∠ CAB,  β  =  ∠ ABC,  γ  =  ∠ BCA и  δ  =  ∠ COP. Пусть точки K и P симметричны точкам A и P соответственно относительно серединного перпендикуляра к отрезку BC. Обозначим через R радиус описанной окружности  ∆ ABC. Тогда OA = OB = OC = OK = R. Кроме того, QP = KA, поскольку KQPA – прямоугольник. Теперь заметим, что  ∠ AOK =  ∠ AOB –  ∠ KOB =  ∠ AOB –  ∠ AOC = 2 γ  – 2 β  ≥ 60 и, учитывая, что OA = OK = R, получим KA ≥ R и QP ≥ R. По неравенству треугольника OP + R = OQ + OC > QC = QP + PC ≥ R + PC. Отсюда следует, что OP > PC и, значит, в  ∆ COP  ∠ POC >  δ . Поскольку  α  = ½ ∠ BOC = ½(180 – 2 ∠ PCO), то действительно  ∠  α  +  ∠  δ  < 90.

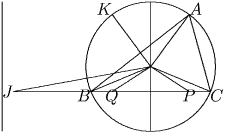
Решение 2

Как и в предыдущем решении, достаточно показать, что OP > PC. Вспомним, что по теореме синусов AB = 2R sin  γ  и AC = 2R sin  β . Отсюда получаем: BP – PC = AB cos  β  – AC cos  γ  = 2R( sin  γ  cos  β  –  sin  β  cos  γ ) = 2R sin ( γ  –  β ). Учитывая, что 30 ≤  γ  –  β  <  γ  < 90, видим, что BP – PC ≥ R. Значит R + OP = BO + OP > BP ≥ R + PC, откуда OP > OC, что и требовалось.

Решение 3

Сначала докажем, что R² > CP • CB. Для этого, поскольку CB = 2R sin  α  и CP = AC cos  γ , достаточно показать, что ¼ >  sin  α  sin  β  cos  γ . Заметим, что 1 >  sin  α  =  sin ( γ  +  β ) =  sin  γ  cos  β  +  sin  β  cos  γ  и ½ ≤  sin ( γ  –  β ) =  sin  γ  cos  β  –  sin  β  cos  γ , поскольку 30 ≤  γ  –  β  < 90. Отсюда следует, что ¼ >  sin  β  cos  γ  и ¼ >  sin  α  sin  β  cos  γ .

Теперь отметим точку J на BC так, что CJ • CP = R². Тогда CJ > CB (поскольку R² > CP • CB), поэтому  ∠ OBC >  ∠ OJC. Из того, что OC/CJ = PC/CO и  ∠ JOC =  ∠ OCP, следует, что  ∆ JCO подобен  ∆ OCP и  ∠ OJC =  ∠ POC =  γ . Значит  δ  <  ∠ OBC = 90 –  α , то есть  α  +  δ  < 90.

Задача 2: Докажите, что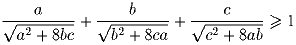

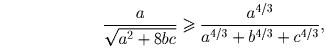
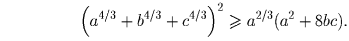
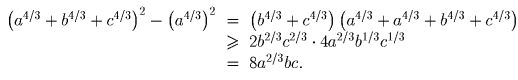
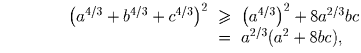
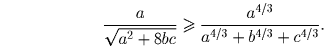
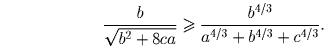
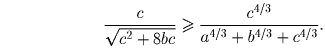
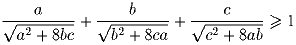
для всех положительных вещественных чисел a, b и c.

Решение: Сначала докажем, что

или, что то же самое,

По неравенству о средних

Отсюда

значит

точно также

и

Сложив эти три неравенства, получим:

Комментарий. Можно доказать, что для любых a,b,c > 0 и  λ  ≥ 8 выполняется следующее неравенство:

Задача 3: Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе.

• Каждый участник решил не более шести задач.
• Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими.

Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.

Решение:

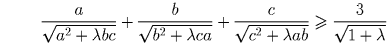
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков. Будем считать задачу «красной», если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков). Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику. Тогда каждая клетка соответствует паре «мальчик–девочка». Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец. По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 • 10 + 21 • 10 < 21²).

Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток. Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками. Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой. В силу первого условия никаких других задач девочка не решала, но тогда максимум 12 мальчиков имеют общие решённые задачи с этой девочкой, что противоречит второму условию.

Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.

Задача 4: Пусть N – нечетное натуральное число большее 1, а k₁, k₂,…k_n – произвольные целые числа. Для каждой из n! перестановок a = (a₁,a₂, … ,a_n) чисел 1, 2,…n, обозначим

Докажите, что найдутся две такие перестановки b и c (b ≠ c), что n! является делителем S(b) – S(c).

Решение:

Пусть  ∑ S(a) – сумма S(a) по всем n! перестановкам a = (a₁,a₂, … a_n). Мы вычислим  ∑ S(a) двумя способами и достигнем противоречия в случае, если n нечётно.

Первый способ. В  ∑ S(a) число k₁ умножается на каждое i ∈ 1, … ,n всего (n – 1)! раз, по одному на каждую перестановку 1,2, … n, в которой a₁ = i. Поэтому коэффициент при k₁ в  ∑ S(a) равен (n – 1)!(1 + 2 +  …  + n) = (n + 1)!/2. Это верно для всех k_i, поэтому

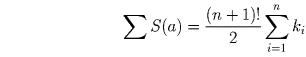
Второй способ. Если n! не является делителем S(b) – S(c) для любого b ≠ c, то все суммы S(a) должны иметь различные остатки при делении на n!. Поскольку всего перестановок n!, эти остатки в точности равны 0, 1, …, n! – 1. Поэтому

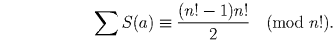
Таким образом

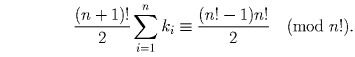
Но для нечётных n левая часть этого сравнения сравнима с 0 по модулю n!, в то время как при n > 1 правая часть не может быть сравнима с 0 (поскольку n! – 1 нечётно). Мы получили противоречие для всех нечётных n > 1.

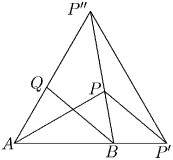
Задача 5: В треугольнике ABC проведена биссектрисы AP и BQ. Известно, что  ∠ BAC = 60 и что AB + BP = AQ + QB. Какими могут быть углы треугольника ABC?

Решение: Обозначим углы треугольника ABC через  α  =  ∠ A = 60,  β  =  ∠ B и  γ  =  ∠ C. Продолжим сторону AB до точки P′ так, чтобы BP′ = BP и построим точку P″ на AQ так, чтобы AP″ = AP′. Тогда BP′P – равнобедренный треугольник с углами при основании равными  β /2. Поскольку AQ + QP″ = AB + BP′ = AB + BP = AQ + QB, отсюда следует, что QP″ = QB. Учитывая, что  ∆ AP′P″ равносторонний, а AP – биссектриса угла A, получаем, что PP′ = PP″.

Докажем, что точки B, P и P″ лежат на одной прямой (а, значит, точка P″ совпадает с точкой C. Предположим, что это не так, то есть  ∆ BPP″ – невырожденный. Тогда  ∠ PBQ =  ∠ PP′B =  ∠ PP″Q =  β /2, а  ∠ QP″B =  ∠ QBP″. Значит  ∠ PP″B =  ∠ PBP″, то есть BP = PP″. Тогда треугольник BPP″ – равносторонний, но из этого следует, что  β /2 = 60, и, значит,  α  +  β  = 60 + 120 = 180. Противоречие.

Поскольку треугольник BCQ равнобедренный, то 120 –  β  =  γ  =  β /2, поэтому  β  = 80 и  γ  = 40.

Задача 6: Пусть a, b, c, d – целые числа такие, что a > b > c > d > 0. Предположим, что ac + bd = (b + d + a – c)(b + d – a + c). Докажите, что число ab + cd составное.

Решение: Предположим, что число ab + cd – простое. Заметим, что ab + cd = (a + d)c + (b – c)a = m •  НОД (a + d,b – c) дл некоторого натуральго m. По предположению или m = 1 или  НОД (a + d,b – c) = 1. Рассмотрим эти варианты по-очереди.

1 случай: m = 1. Тогда

что неверно.

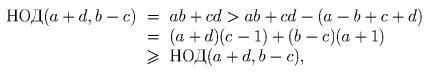
2 случай:  НОД (a + d,b – c) = 1. Подставляя ac + bd = (a + d)b – (b – c)a в левую часть равенства ac + bd = (b + d + a – c)(b + d – a + c), получаем (a + d)(a – c – d) = (b – c)(b + c + d).

Ввиду этого, найдётся такое натуральное число k, что

Складывая эти равенства, получаем, что a + b = k(a + b – c + d) и, следовательно, k(c – d) = (k – 1)(a + b). Вспомним, что a > b > c > d. Если k = 1, то c = d – противоречие. Если k ≥ 2, то

противоречие.

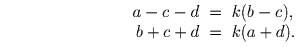
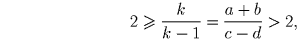
В обоих случаях достигнуто противоречие, значит число ab + cd составное.