 |
 |
|
| Задачная база >> Международные соревнования >> Математические соревнования северных стран >> 1996 | Показать решения |
|
|
| Международные соревнования. Математические соревнования северных стран. 1996 |
|
|
Докажите, что существует число делящееся на 1996 сумма цифр которого равна 1996.
Задача 2:
Найдите все вещественные x для которых xn + x – n целое при любом n.
Задача 3:
Окружность, имеющая своим диаметром высоту AH треугольника ABC пересекает стороны AB и AC в точках D и E соответственно. Докажите, что центр окружности описанной около треугольника ABC лежит на прямой, содержащей высоту AK треугольника ADE.
Задача 4:
Вещественнозначная функция f определенная на множестве натуральных чисел и натуральное число a удовлетворяют следующим соотношениям
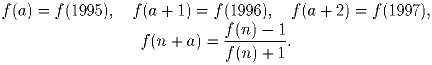
| Задачная база >> Международные соревнования >> Математические соревнования северных стран >> 1996 | Показать решения |