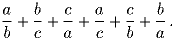Задача 1: Числа a, b, c отличны от нуля, а их сумма равна нулю. Найдите значение выражения

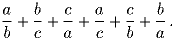
Задача 2: Несколько учащихся ушли из лицея и несколько пришли. В результате число учащихся уменьшилось на 10, а доля мальчиков в лицее увеличилась с 50 до 55. Увеличилось или уменьшилось число мальчиков?

Задача 3: В параллелограмме ABCD точка E — середина AD. Точка F — основание перпендикуляра, опущенного из B на прямую CE. Докажите, что треугольник ABF равнобедренный.

Задача 4: Барон Мюнхгаузен утверждает, что пустил шар от борта бильярда, имеющего форму правильного треугольника, так, что тот, отражаясь от бортов, прошел через некоторую точку три раза в трех различных направлениях и вернулся в исходную точку. Могут ли слова барона быть правдой? (Отражение шара от борта происходит по закону «угол падения равен углу отражения».)

Задача 5: Имеется 201 гиря, веса которых (в граммах) — последовательные натуральные числа от 1 до 201. Назовем гирю хорошей, если после ее удаления оставшиеся 200 гирь можно разделить на две группы, равные по весу и по количеству гирь. Докажите, что

а) гиря 101 г хорошая;

б) гиря 199 г хорошая.