 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 11 класс | Убрать решения |
|
|
| 64 Московская математическая олимпиада. Городской тур. 11 класс |
|
|
Существуют ли три квадратных трёхчлена, такие что каждый из них имеет два различных действительных корня, а сумма любых двух трёхчленов не имеет действительных корней?
(А. Канель)
Решение: =1Ответ: да, существуют. Например, таковыми являются многочлены (x – 10)² – 1, x² – 1 и (x + 10)² – 1.
Задача 2:Дана геометрическая прогрессия. Известно, что её первый, десятый и тридцатый члены являются натуральными числами. Верно ли, что её двадцатый член также является натуральным числом?
(Фольклор)
Решение: =2Ответ: да, верно. Пусть a1, a2, …, an, … – данная
геометрическая
прогрессия, q – её знаменатель. По условию a1, a10 = a1q9
и a30 = a1q29 –
натуральные числа. Поэтому q9 и q29 – положительные рациональные
числа. Отсюда следует, что 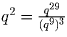 –
положительное рациональное
число и
–
положительное рациональное
число и 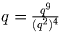 – также положительное рациональное число.
– также положительное рациональное число.
Пусть 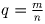 , где m и n – натуральные взаимно простые числа. Число
, где m и n – натуральные взаимно простые числа. Число
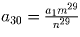 натуральное, m29 и n29
взаимно просты, следовательно, a1
делится на n29. Отсюда получаем, что
натуральное, m29 и n29
взаимно просты, следовательно, a1
делится на n29. Отсюда получаем, что
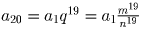 –
число
натуральное.
–
число
натуральное.
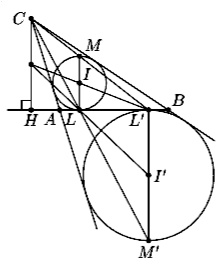
В треугольнике ABC точка I – центр вписанной окружности, I′ – центр окружности, касающейся стороны AB и продолжений сторон CB и CA; L и L′ – точки, в которых сторона AB касается этих окружностей. Докажите, что прямые IL′, I′L и высота CH треугольника ABC пересекаются в одной точке.
(А. Заславский)
Решение: =3Обозначим через M точку вписанной окружности, диаметрально противоположную точке L, через M′ – точку вневписанной окружности, диаметрально противоположную точке L′ (рис.). Таким образом, ML и M′L′ – диаметры, соответственно, вписанной и вневписанной окружностей, они параллельны высоте CH треугольника ABC. Вписанная окружность переходит во вневписанную при гомотетии с центром в точке C. При этой гомотетии диаметр ML переходит в параллельный ему диаметр, т.е. M′L′. Поэтому точки C, M, L′ лежат на одной прямой, а также точки C, M′, L лежат на одной прямой. Отсюда следует, что треугольники L′LM и L′HC совмещаются гомотетией с центром в точке L′. Поскольку L′I – медиана треугольника L′LM, прямая L′I пересекает отрезок CH в его середине.
Далее, треугольники LL′M′ и LHC совмещаются гомотетией с центром в точке L. Поскольку LI′ является медианой в треугольнике LL′M′, прямая LI′ также пересекает отрезок CH в его середине, откуда следует утверждение задачи.
Докажите, что не существует многочлена степени не ниже двух с целыми неотрицательными коэффициентами, значение которого при любом простом p является простым числом.
(А. Канель)
Решение: =4Предположим, что такой многочлен Q(x) существует. Пусть Q(x) = anxn + an – 1xn – 1 + … + a1x + a0, где a0, a1, , an – целые неотрицательные числа, an не равно 0, n > 2.
Если a0 = 0, то Q(x) = x(anxn – 1 + an – 1xn – 2 + … + a1), следовательно, при простом p число Q(p) делится на p и больше p (здесь используется то, что степень Q не меньше 2), поэтому Q(p) – число составное. Допустим, a0 ≥ 2. Обозначим через p некоторый простой делитель a0. Тогда Q(p) = (anpn – 1 + an – 1pn – 2 + … + a1)p + a0 делится на p и больше p, значит, Q(p) – число составное. Таким образом, имеется единственная возможность: a0 = 1.
Если для любого простого p число Q(p) простое, то и число Q(Q(p)) является простым при любом простом p. Значит, свободный член многочлена Q(Q(x)) должен равняться 1. Однако, поскольку Q(0) = a0 = 1, Q(Q(0)) = an + an – 1 + … + a1 + 1 > 1. Мы получили противоречие, завершающее доказательство.
Задача 5:
Докажите, что в пространстве существует расположение 2001 выпуклого многогранника, такое что никакие три из многогранников не имеют общих точек, а любые два касаются друг друга (т. е. имеют хотя бы одну граничную точку, но не имеют общих внутренних точек).
(А. Канель)
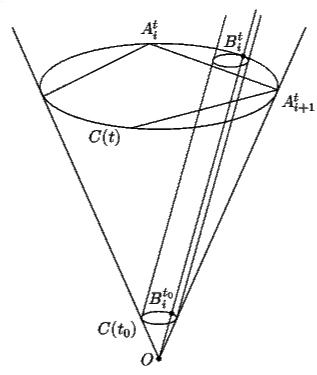
Решение: =5Положим N = 2001 и опишем построение расположения N выпуклых многогранников, из которых никакие три не пересекаются и любые два касаются.
Рассмотрим бесконечный круговой конус, вершина O
которого находится в начале координат, а ось направлена вдоль оси Oz.
На окружности, являющейся сечением конуса плоскостью z = 1, возьмём точки
A1, A2, , AN – вершины правильного N-угольника.
Обозначим через B1,
B2, , BN середины меньших дуг A1A2, A2A3, …, ANA1
соответственно. Через C(t) обозначим круг, являющийся сечением конуса
плоскостью z = t,
через Ot – центр этого круга, через 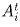 ,
, 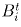 – точки
пересечения
образующих OAi, OBi с кругом C(t), где t > 0, 1 < i < N.
– точки
пересечения
образующих OAi, OBi с кругом C(t), где t > 0, 1 < i < N.
Докажем вспомогательное утверждение.
Лемма. Пусть выпуклый многоугольник M лежит внутри круга C(t0),
t0 > 0.
Рассмотрим бесконечную вверх «призму» P, основанием которой служит
многоугольник M, а боковое «ребро» параллельно прямой OBi для некоторого
i. Многоугольник (равный M), который получается при пересечении призмы P и
круга C(t), обозначим M(t) (таким образом, M(t0) совпадает с M). Тогда
найдётся такое положительное T > t0, что при всех t > T многоугольник M(t)
будет содержаться внутри сегмента 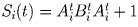 круга C(t).
круга C(t).
Доказательство. Многоугольник M(t) является образом M при параллельном
переносе на вектор, параллельный образующей OBi. Поэтому многоугольник
M(t) содержится внутри круга, равного кругу C(t0), который касается круга
C(t) в точке 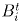 . Расстояние от точки
. Расстояние от точки 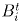 до прямой
до прямой
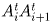 прямо
пропорционально длине образующей OBti; следовательно, найдется такое T,
что при всех t > T это расстояние больше диаметра окружности C(t0). Это
и означает, что многоугольник M(t) попадает внутрь сегмента Si(t)
круга C(t). Лемма доказана.
прямо
пропорционально длине образующей OBti; следовательно, найдется такое T,
что при всех t > T это расстояние больше диаметра окружности C(t0). Это
и означает, что многоугольник M(t) попадает внутрь сегмента Si(t)
круга C(t). Лемма доказана.
Переходим к индуктивному построению нашего расположения.
Выберем t1 > 0. Возьмём выпуклый многоугольник M1 внутри круга C(t1). Рассмотрим бесконечную вверх «призму» P + 1, основанием которой служит многоугольник M1, а боковое «ребро» параллельно прямой OB1.
Пусть для некоторого n (1 < n < N) уже определены положительные числа t1, t2, …, tn – 1, t1 < t2 < … < tn – 1, выпуклые многоугольники M1, …, Mn – 1, лежащие внутри кругов C(t1), C(t2), …, C(tn – 1), бесконечные «призмы» P1, P2, …, Pn – 1 с основаниями M1, M2, …, Mn – 1 и боковыми «рёбрами», параллельными OB1, OB2, …, OBn – 1 соответственно.
Согласно лемме, существует число tn > tn – 1, такое что многоугольник M1(tn) содержится внутри сегмента S1(tn) круга C(tn), многоугольник M2(tn) содержится внутри сегмента S2(tn) круга C(tn), …, многоугольник Mn – 1(tn) содержится внутри сегмента Sn – 1(tn) круга C(tn).
Сдвигаем каждую из прямых 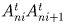 (1 < i < n – 1) в направлении
вектора
(1 < i < n – 1) в направлении
вектора
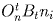 , пока она не совпадёт с прямой li(tn),
касающейся многоугольника
Mi(tn). Теперь построим выпуклый многоугольник Mn, который содержится в
круге C(tn), касается каждого многоугольника Mi(tn) и лежит по разные с
ним стороны от прямой li(tn): возьмём для каждого i
одну из точек касания
многоугольника Mi(tn) и прямой li(tn); при n > 3 эти точки являются
вершинами выпуклого (n – 1)-угольника, который и можно выбрать в качестве
Mn; при n = 2,3 надо добавить ещё несколько точек).
, пока она не совпадёт с прямой li(tn),
касающейся многоугольника
Mi(tn). Теперь построим выпуклый многоугольник Mn, который содержится в
круге C(tn), касается каждого многоугольника Mi(tn) и лежит по разные с
ним стороны от прямой li(tn): возьмём для каждого i
одну из точек касания
многоугольника Mi(tn) и прямой li(tn); при n > 3 эти точки являются
вершинами выпуклого (n – 1)-угольника, который и можно выбрать в качестве
Mn; при n = 2,3 надо добавить ещё несколько точек).
Рассмотрим бесконечную вверх «призму» Pn, основанием которой является многоугольник Mn, а боковое «ребро» параллельно прямой OBn. Построение будет закончено, когда мы получим призмы P1, P2, …, PN. Наконец, «срежем» призмы плоскостью z = T, где T > tN.
Докажем, что полученные (обычные) призмы удовлетворяют условию задачи. Для
этого достаточно показать, что призма Pn пересекается с призмой Pi,
i < n,
только в плоскости круга C(tn). Пусть, напротив, найдётся общая точка
R ∈ C(t) двух призм, где t > tn. Через точку R проведём прямые, параллельные
OBn и OBi; обозначим их точки пересечения с плоскостью круга C(tn) через
Rn и Ri соответственно. Тогда точка Rn должна принадлежать многоугольнику
Mn(tn), а точка Ri должна принадлежать многоугольнику Mi(tn).
Ясно, что
(ненулевые) векторы RiRn и 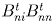 противоположно направлены.
противоположно направлены.
Однако это невозможно, поскольку точки Ri и Btni
лежат по одну сторону от
прямой li(tn), а точки Rn и 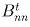 – по другую. Противоречие
завершает доказательство.
– по другую. Противоречие
завершает доказательство.
Задача 6:
По кругу расставлено несколько коробочек. В каждой из них может лежать один или несколько шариков (или она может быть пустой). За один ход разрешается взять все шарики из любой коробочки и разложить их, двигаясь по часовой стрелке, начиная со следующей коробочки, кладя в каждую коробочку по одному шарику.
а) Докажите, что если на каждом следующем ходе шарики берут из той коробочки, в которую попал последний шарик на предыдущем ходе, то в какой-то момент повторится начальное размещение шариков.
б) Докажите, что за несколько ходов из любого начального размещения шариков по коробочкам можно получить любое другое.
(В. Гуровиц)
Решение: =6а) Текущее состояние описанной в задаче системы определяется количеством шариков в каждой коробочке и указанием коробочки, с которой нужно начинать раскладывать шарики в следующий раз. Поэтому возможных состояний системы конечное число. Из каждого состояния можно, раскладывая шарики, перейти в другое состояние системы, которое определено однозначно. Наоборот, зная состояние системы в настоящий момент, можно однозначно определить состояние системы перед последним раскладыванием шариков. Действительно, последнее раскладывание должно было закончиться на выделенной коробочке; поэтому, чтобы восстановить предыдущее состояние, нужно взять один шарик из выделенной коробочки и далее, идя против часовой стрелки, брать по шарику из каждой коробочки, пока это возможно. Когда же мы встретим пустую коробочку, мы положим в неё все собранные шарики и объявим её отмеченной. (Фактически мы дали описание операции, обратной к ходу, описанному в условии задачи.) Если обозначить состояния системы точками, а возможность перехода из одного состояния в другое – стрелкой, соединяющей соответствующие точки (т. е. построить граф состояний системы), то из каждой точки будет выходить ровно одна стрелка и в каждую точку будет входить ровно одна стрелка. Начнём двигаться по стрелкам, начиная с заданного состояния A1. Получаем последовательность состояний A2, A3 …Поскольку число состояний конечно, в некоторый момент в последовательности Ai возникнет повторение. Пусть, например, Ak = An, где k < n. Поскольку в точку Ak входит ровно одна стрелка, из равенства Ak = An следует Ak – 1 = An – 1, ..., A1 = Ak – n + 1. Тем самым, через n – k ходов мы вернулись в состояние A1.
б) В отличие от задачи а) теперь состояние системы определяется лишь тем, как разложены шарики по коробочкам. В каждый момент возможно несколько ходов, а именно столько, сколько в данный момент имеется непустых коробочек. Очевидно, имеется столько же возможностей выполнить обратную операцию, описанную в решении пункта а). В терминах графа состояний системы это означает, что из каждой точки выходит столько же стрелок, сколько в неё входит.
Докажем два вспомогательных утверждения.
1) При любом начальном состоянии можно добиться того, чтобы все шарики оказались в одной наперёд заданной коробочке M.
В самом деле, если при каждой операции брать шарики из непустой коробочки, ближайшей к M при движении против часовой стрелки, то либо число шариков в M увеличится, либо ближайшая к M непустая коробочка станет ещё ближе, что не может продолжаться бесконечно. Утверждение доказано.
Обозначим через K состояние, при котором все шарики собраны в коробочке M, и через B некоторое произвольное состояние.
2) Из B можно пройти в K, двигаясь по стрелкам против их направления (по обратным стрелкам).
Действительно, согласно предыдущему утверждению, найдётся такая последовательность (различных) состояний B = A1,A2, … ,An = K, что точки A1, A2, …, An последовательно соединены стрелками. Будем двигаться по обратным стрелкам из An в An – 1, из An – 1 в An – 2, …, из A2 в A1 и далее из A1, пока это возможно, выбирая на каждом шаге обратную стрелку, по которой мы ещё не проходили. Остановиться мы можем только в K. В самом деле, предположим, что при движении мы стираем стрелки. Cначала в каждую точку входило столько же стрелок, сколько выходило из неё. При стирании стрелок в каждый момент времени в каждую точку, за исключением начальной точки K, входит не меньше стрелок, чем выходит. Следовательно, если мы вошли в некоторую точку (кроме K) по обратной стрелке, то мы сможем и выйти из неё. Отсюда следует, что из B можно пройти в K по обратным стрелкам, т.е. из K можно пройти в B по обычным стрелкам.
Теперь нетрудно завершить доказательство. Пусть имеются два произвольных состояния A и B. Чтобы пройти, двигаясь по стрелкам, из A в B, можно вначале пройти из A в K, а затем из K в B. Как мы доказали, и то и другое возможно.
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 11 класс | Убрать решения |