 |
 |
|
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 8 класс | Показать решения |
|
|
| 64 Московская математическая олимпиада. Городской тур. 8 класс |
|
|
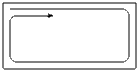
На клетчатой бумаге нарисован прямоугольник шириной 200 и высотой 100 клеток. Его закрашивают по клеткам, начав с левой верхней и идя по спирали (дойдя до края или уже закрашенной части, поворачивают направо, рис. 2). Какая клетка будет закрашена последней? (Укажите номер её строки и столбца. Например, нижняя правая клетка стоит в 100-й строке и 200-м столбце.)
(A. Хачатурян)
Задача 2:Можно ли поставить на плоскости 100 точек (сначала первую, потом вторую и так далее до сотой) так, чтобы никакие три точки не лежали на одной прямой и чтобы в любой момент фигура, состоящая из уже поставленных точек, имела ось симметрии?
(И. Акулич)
Задача 3:Даны шесть слов:
ЗАНОЗА
ЗИПУНЫ
КАЗИНО
КЕФАЛЬ
ОТМЕЛЬ
ШЕЛЕСТ
За один шаг можно заменить любую букву в любом из этих слов на любую другую (например, за один шаг можно получить из слова ЗАНОЗА слово ЗКНОЗА. Сколько шагов нужно, чтобы сделать все слова одинаковыми (допускаются бессмысленные)? Приведите пример и докажите, что меньшим числом шагов обойтись нельзя.
(В. Доценко, А. Шень)
Задача 4:В треугольнике ABC проведены биссектриса AK, медиана BL и высота CM. Треугольник KLM равносторонний. Докажите, что треугольник ABC равносторонний.
(Р. Женодаров)
Задача 5:Лёша задумал двузначное число (от 10 до 99). Гриша пытается его отгадать, называя двузначные числа. Считается, что он отгадал, если одну цифру он назвал правильно, а в другой ошибся не более чем на единицу (например, если задумано число 65, то 65, 64 и 75 подходят, а 63, 76 и 56 – нет). Придумайте способ, гарантирующий Грише успех за 22 попытки (какое бы число ни задумал Лёша).
(Фольклор)
Задача 6:Лёша задумал двузначное число (от 10 до 99). Гриша пытается его отгадать, называя двузначные числа. Считается, что он отгадал, если одну цифру он назвал правильно, а в другой ошибся не более чем на единицу (например, если задумано число 65, то 65, 64 и 75 подходят, а 63, 76 и 56 – нет). Покажите, что нет способа, гарантирующего Грише успех за 18 попыток.
(Фольклор)
| Задачная база >> Московские соревнования >> Городская олимпиада >> 2001 >> Городской тур >> 8 класс | Показать решения |