Задача 1: Напомним правила игры «Жизнь». На клетчатом листе стоит несколько
фишек. Их расположение во всех клетках одновременно меняется следующим образом.
Если в клетках, соседних с данной (по стороне или углу), стоит ровно 3 фишки, то
в данную клетку ставится фишка (если ее не было). Если в соседних клетках более
3 или менее 2 фишек, то фишка снимается (если она была). Если в соседних клетках
ровно 2 фишки, то состояние клетки не меняется.
Докажите, что в игре «Жизнь» на квадрате 2001 × 2001
существует конфигурация, не имеющая прообраза.
Задача 2: Докажите, что равенство
|x! – yy| = n при любом натуральном n
имеет лишь конечное число решений в натуральных числах x, y.
Задача 3: Дан треугольник ABC. На прямой AB отметим точку
C′. Вокруг треугольников ACC′ и BCC′ опишем окружности и
отметим вторые точки A′ и B′ их пересечения с прямыми BC и
AC соответственно. Вокруг треугольников A′AB и ABB′
опишем окружности и отметим их вторые точки пересечения B″ и A″
с прямыми AC и BC и т.д. Сколько точек будет отмечено на прямой
AB после построения 2001 окружности?
Задача 4:
Существует ли такая функция f(x), определенная на
всей оси и отличная от константы, что при всех x, y, z
выполнено неравенство
f(x + y) + f(y + z) + f(z + x) ≥ 4f(x + 2y + 3z)?
Задача 5:
Единичный квадрат разбит на три многоугольника. Докажите, что
диаметр хотя бы одного из них не меньше
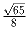
.
Задача 6:
На плоскости отмечено 6 точек, никакие три из которых не лежат на
одной прямой, причём все попарные расстояния между ними различны. Докажите, что
среди треугольников с вершинами в этих точках найдутся два треугольника с общей
стороной такой, что для одного эта сторона является наибольшей, а для другого -
наименьшей.


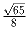 .
Задача 6:
На плоскости отмечено 6 точек, никакие три из которых не лежат на
одной прямой, причём все попарные расстояния между ними различны. Докажите, что
среди треугольников с вершинами в этих точках найдутся два треугольника с общей
стороной такой, что для одного эта сторона является наибольшей, а для другого -
наименьшей.
.
Задача 6:
На плоскости отмечено 6 точек, никакие три из которых не лежат на
одной прямой, причём все попарные расстояния между ними различны. Докажите, что
среди треугольников с вершинами в этих точках найдутся два треугольника с общей
стороной такой, что для одного эта сторона является наибольшей, а для другого -
наименьшей.