Задача 1:
Постройте график уравнения
|y| = (1 – cos ²x)
1/2/( sin x)
Задача 2:
Известно, что положительное число a является
одним из корней уравнения
x(x + 1)(x + 2)...(x + 100) = 1.
Докажите, что
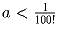
.
(Напомним, что n! = 1*2*3*...*(n – 1)*n)
Задача 3:
Основания трапеции равны 3 см и 5 см.
Одна из диагоналей трапеции равна 8 см, угол между диагоналями
равен 60. Найдите периметр трапеции.
Задача 4:
Сколько пар (x,y) целых чисел
являются решениями уравнения
(x² + x + 1)² + (y² – y + 1)² = 2002²?
Задача 5:
Отрезок AB длиной 8 см лежит в плоскости
α . Точка M находится на расстоянии 10 см
от ближайшей к ней точки отрезка AB и на расстоянии 6 см от
плоскости α . Точка O – проекция точки M
на плоскость α . Найдите площадь треугольника
AOB, если известно, что один из углов этого треугольника равен
150.
Задача 6:
Один математик говорит другому: «Я думаю, ты сможешь
узнать, сколько у меня внуков и сколько лет исполнилось каждому, если
я сообщу тебе, что произведение их возрастов равно 36, а сумма –
количеству этажей в доме напротив». «Этой информации не
достаточно!» – возражает второй. Тогда первый добавляет:
«Старшего внука зовут Вася». «Теперь другое дело!» – говорит
второй и даёт правильный ответ. Дайте его и вы. Объясните.


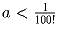 .
(Напомним, что n! = 1*2*3*...*(n – 1)*n)
.
(Напомним, что n! = 1*2*3*...*(n – 1)*n)