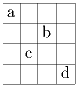
Задача 1: В некоторых клетках квадрата 4 × 4 расставлены буквы a, b, c и d (смотри рисунок). Заполните теми же буквами остальные клетки так, чтобы в каждом столбце и в каждой строке каждая буква встречалась ровно один раз.

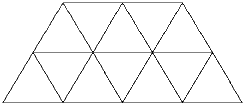
Задача 2: Разрежьте фигуру, изображённую на рисунке, на 4 равные части (одинаковые по форме и по размеру).

Задача 3: В бак, имеющий форму куба, выливают ведро воды (10 литров). Каков будет уровень воды в баке, если ребро куба имеет длину 1 метр?

Задача 4: Волк и Заяц устроили забег на стадионе. Встав рядом, они одновременно стартовали в одном направлении. Известно, что скорость Волка в 2 раза больше скорости Зайца. Сколько кругов успеет пробежать Заяц до тех пор, пока его снова не догонит Волк?

Задача 5: Винни-Пух и Пятачок играют в слова. Винни-Пух придумал 10 слов, а Пятачок - только 5. Они по очереди называют по одному слову, не повторяя уже названные. Проигрывает тот, кто не сможет назвать слово. Начинал Винни-Пух, а выиграл Пятачок. Придумайте за них слова и укажите, в каком порядке они могли их называть.