Задача 1:
Числитель дроби увеличили на 3, а знаменатель – на 8.
Могла ли получиться дробь, равная исходной? Ответ обоснуйте.
Задача 2:
На стороне AC треугольника ABC отметили точку
E. Известно, что периметр треугольника ABC равен 25 см,
периметр треугольника ABE – 15 см, а периметр
треугольника BCE – 17 см. Найдите длину отрезка BE.
Задача 3:
Решите уравнение
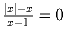 Задача 4:
Задача 4:
В городе Глупове живут только полицейские, воры и обыватели.
Полицейские всегда врут обывателям, воры – полицейским, а обыватели –
ворам.
Во всех остальных случаях жители Глупова говорят правду.
Однажды несколько глуповцев водили хоровод и каждый сказал своему правому
соседу: «Я - полицейский». Сколько обывателей было в этом хороводе?
Задача 5:
В мешке у Деда Мороза лежат конфеты трёх видов: шоколадные,
ириски и леденцы. Дед Мороз знает, что если вынуть любые 100 конфет из мешка,
то среди них обязательно найдутся конфеты всех трёх видов.
Какое наибольшее количество конфет может быть в мешке у Деда Мороза?


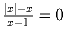 Задача 4:
В городе Глупове живут только полицейские, воры и обыватели.
Полицейские всегда врут обывателям, воры – полицейским, а обыватели –
ворам.
Во всех остальных случаях жители Глупова говорят правду.
Однажды несколько глуповцев водили хоровод и каждый сказал своему правому
соседу: «Я - полицейский». Сколько обывателей было в этом хороводе?
Задача 5:
В мешке у Деда Мороза лежат конфеты трёх видов: шоколадные,
ириски и леденцы. Дед Мороз знает, что если вынуть любые 100 конфет из мешка,
то среди них обязательно найдутся конфеты всех трёх видов.
Какое наибольшее количество конфет может быть в мешке у Деда Мороза?
Задача 4:
В городе Глупове живут только полицейские, воры и обыватели.
Полицейские всегда врут обывателям, воры – полицейским, а обыватели –
ворам.
Во всех остальных случаях жители Глупова говорят правду.
Однажды несколько глуповцев водили хоровод и каждый сказал своему правому
соседу: «Я - полицейский». Сколько обывателей было в этом хороводе?
Задача 5:
В мешке у Деда Мороза лежат конфеты трёх видов: шоколадные,
ириски и леденцы. Дед Мороз знает, что если вынуть любые 100 конфет из мешка,
то среди них обязательно найдутся конфеты всех трёх видов.
Какое наибольшее количество конфет может быть в мешке у Деда Мороза?