Задача 1:
От причала A к причалу B отошли катер и лодка.
Известно, что они плыли с постоянными скоростями, причём скорость катера была
в 5 раз больше, чем скорость лодки, но катер сделал несколько остановок.
Сколько времени катер затратил на остановки, если на путь от A до
B он затратил 2 часа, а лодка – 4 часа?
Задача 2:
Решите уравнение
x³ + 5x² + 2x = 8
Задача 3:
В выпуклом четырёхугольнике ABCD
точки M и N – середины сторон AB и CD
соответственно. Известно, что
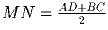
.
Верно ли, что AD\|BC?
Задача 4:
На острове живут только рыцари (которые всегда говорят правду)
и лжецы (которые всегда лгут). Трое из них сделали по два заявления.
Первый сказал: «На острове живёт не более 3 человек»,
«Все жители острова - лжецы»;
Второй сказал: «На острове живёт не более 4 человек»;
«Не все жители острова - лжецы»;
Третий сказал: «На острове живёт 5 человек»;
«На острове не менее 3 лжецов»
Сколько человек живёт на острове и сколько среди них лжецов?
Задача 5:
В треугольнике ABC высоты AA
1 и
CC
1 пересекаются в точке H, лежащей внутри
треугольника. Известно, что H – середина AA
1,
а CH:HC
1 = 2:1.
Найдите величину угла B.
Задача 6:
У Васи было 20 настоящих монет и 21 фальшивая.
Каждая фальшивая монета на 1 грамм легче настоящей.
Одну монету Вася потерял.
Есть чашечные весы, которые показывают, на сколько грамм
одна чаша перевешивает другую.
Как определить за одно взвешивание, какая монета потерялась?


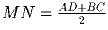 .
Верно ли, что AD\|BC?
Задача 4:
На острове живут только рыцари (которые всегда говорят правду)
и лжецы (которые всегда лгут). Трое из них сделали по два заявления.
.
Верно ли, что AD\|BC?
Задача 4:
На острове живут только рыцари (которые всегда говорят правду)
и лжецы (которые всегда лгут). Трое из них сделали по два заявления.