Задача 1:
Существует ли простое число p, такое что число
3p + 2001 тоже простое?
Задача 2:
Решить неравенство
x¹º + x
6 + x
5 + x³ + x² + x + 1 > 0
Задача 3:
Дано два непересекающихся круга. Существует ли вне этих кругов
такая точка, что всякая прямая, проходящая через неё, пересекает хотя бы один
из данных кругов?
Задача 4:
Задача 5:
В прямоугольном треугольнике ABC на гипотенузу опущена
высота CD. Доказать, что сумма длин радиусов окружностей, вписанных в
треугольники ABC, ACD и CBD равна длине CD.
Задача 6:
Составьте из бесконечного набора чисел
2
– 1,2
– 2, … ,2
– n, …
геометрическую прогрессию, сумма которой будет равна
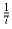
.
Ответ обосновать.


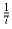 .
Ответ обосновать.
.
Ответ обосновать.