 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1979 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1979 |
|
|
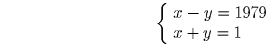

Задача 2: (6–8) В соревнованиях участвуют 10 фигуристов. Соревнования судят трое судей следующим способом: каждый судья по-своему распределяет между фигуристами места (с первого по десятое), после чего победителем считается фигурист с наименьшей суммой мест. Какое наибольшее значение может принимать эта сумма у победителя (победитель единственный)? Решение: Докажем, что искомое наибольшее значение суммы мест победителя равно 15. Для этого необходимо доказать два утверждения. Первое: при любом варианте судейства сумма мест победителя не может быть больше 15. Второе: существует такой вариант судейства, при котором сумма мест победителя равна 15.
Докажем сначала первое утверждение. Для этого посчитаем двумя способами сумму мест, присужденных всеми судьями всем участникам соревнований. С одной стороны, поскольку каждый из трех судей распределил набор мест с первого по десятое, эта сумма равна 3 • (1 + 2 + ... + 10) = 165. С другой стороны, ее же мы должны получить, сложив сумму мест, полученных каждым фигуристом. Если предположить, что победитель получил сумму не меньше 16, тогда все остальные получили сумму мест не меньше 17, и рассматриваемая общая сумма не меньше, чем 16 + 9 • 17 = 169. Полученное противоречие доказывает, что сумма мест победителя не больше 15.
Для доказательства второго утверждения достаточно привести пример судейства, при котором сумма мест победителя равна 15. Такой пример приведен ниже в виде таблицы:
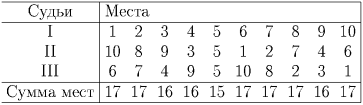
Задача 3: (6–8) В колоде 16 карт, пронумерованных сверху вниз. Разрешается снять часть колоды сверху, после чего снятую и оставшуюся части колоды, не переворачивая «врезать" друг в друга. Может ли случиться, что после нескольких таких операций карты окажутся пронумерованными снизу вверх? Если да, то за какое наименьшее число операций это может произойти?
Решение: Простейший способ осуществить требуемую перестановку — брать карты сверху по одной (это допускается условием задачи) от первой до пятнадцатой и класть на соответствующее место: первую — в самый низ, каждую следующую — между шестнадцатой и предыдущей из положенных карт. Достаточно ясно, что такой способ перестановки за 15 операций не является оптимальным.
Приведем более «хитрый" способ, позволяющий добиться того же результата всего за 4 операции. Каждый раз будем снимать ровно половину колоды — 8 карт сверху и «врезать" снятую часть колоды в оставшуюся «через одну". Трансформация колоды при таких операциях показана на схеме:
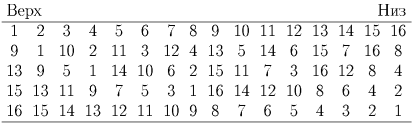
Докажем теперь, что приведенный способ оптимален, т.е. что за три операции такую перестановку осуществить невозможно. Рассмотрим произвольные три операции над колодой, удовлетворяющие условию задачи. При каждой операции колода делится на две части: часть, которая снимается, и часть, которая остается. Поскольку всего карт 16, то одна из этих частей содержит не менее восьми карт. Аналогичное рассуждение показывает, что среди этих карт найдутся по крайней мере четыре, которые при второй операции либо все были в снятой части колоды, либо все в оставшейся. А среди них, в свою очередь, найдутся две карты, оказавшиеся в одной части и при третьей операции. Таким образом, мы нашли две карты, которые при всех операциях либо снимались, либо оставались в колоде вместе. Тем самым порядок этих карт в колоде после трех операций не изменился. Значит, не могло получиться так, что нумерация карт в колоде поменялась на противоположную.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1979 | Убрать решения |