 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1982 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1982 |
|
|
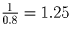 раз больше. Другими
словами, на 25% больше.
раз больше. Другими
словами, на 25% больше.Задача 2: (6) Если класс из 30 человек рассадить в зале кинотеатра, то в любом случае хотя бы в одном ряду окажется не менее двух одноклассников. Если то же самое проделать с классом из 26 человек, то по крайней мере три ряда окажутся пустыми. Сколько рядов в зале? Решение: Первое условие означает, что в зале не более 29 рядов. Действительно, если бы количество рядов было не меньше 30, то, очевидно, класс из 30 человек можно было бы рассадить не более чем по одному на каждый ряд.
Второе условие означает, что количество рядов в зале не менее 29. Действительно, если количество рядов не больше 28, то сажая учеников класса из 26 человек по очереди на пустые ряды, получим, что либо в какой-то момент все ряды будут заняты, либо все 26 учеников будут сидеть по одному на 26 рядах, и в этом случае останутся свободными не более двух рядов.
Значит, в кинотеатре 29 рядов. Очевидно, что в этом случае оба условия задачи выполнены.
Задача 3: (6) В одной из вершин а) октаэдра б) куба сидит муха. Может ли она проползти по всем его ребрам ровно по одному разу и возвратиться в исходную вершину? (Примечание: октаэдр представляет собой две четырехугольные пирамиды, склеенные по основаниям.) Решение: а) Пусть, A, B, C, A1, B1, C1 — вершины октаэдра, причем (A,A1), (B,B1) и (B,B1) — пары противоположных вершин. Тогда любая пара вершин, кроме этих трех, соединяется ребром. Путь мухи может быть следующим: ABA1C1BCAC1B1CA1B1A.
б) В каждой из восьми вершин куба сходится по три ребра. Согласно Т14, из этого следует, что осуществить требуемое путешествие невозможно.
Задача 4:
а) (7–8) Дано шесть натуральных чисел. Все они различны и дают в сумме 22. Найти эти числа и доказать, что других нет.
б) (9) Тот же вопрос про 100 чисел, дающих в сумме 5051.
Решение: Расположим числа в порядке возрастания. Тогда очевидно, что каждое число будет больше своего номера. Найдем сумму номеров всех чисел: а) 1 + 2 + 3 + 4 + 5 + 6 = 21; б) 1 + 2 + … + 100 = 5050. (Последнюю сумму можно посчитать следующим способом: (1 + 100) + (2 + 99) + … + (50 + 51) = 50 • 101 = 5050.) В обоих случаях эта сумма на единицу меньше суммы самих чисел. Значит, одно число на единицу больше своего номера, а остальные — равны ему. Числом, большим своего номера, может быть только последнее. Действительно, если какое-то число больше своего номера, то все последующие числа тоже больше своего номера. Поэтому искомыми числами будут в пункте а) 1, 2, 3, 4, 5, 7; а в пункте б) — 1, 2, …, 99, 101.Задача 5: (7–8) Для того, чтобы застеклить 15 окон различных размеров и форм, заготовлено 15 стекол в точности по окнам (окна такие, что в каждом окне должно быть одно стекло). Стекольщик, не зная, что стекла подобраны, работает так: он подходит к очередному окну и перебирает неиспользованные стекла до тех пор, пока не найдет достаточно большое (то есть либо в точности подходящее, либо такое, из которого можно вырезать подходящее), если же такого стекла нет, то переходит к следующему окну, и так, пока не обойдет все окна. Составлять стекло из нескольких частей нельзя. Какое максимальное число окон может остаться незастекленными? Решение: Покажем сначала, что если в какой-либо момент осталось не меньше 8 окон (и, соответственно, не меньше 8 стекол), то стекло для какого-нибудь окна из оставшихся можно подобрать. Действительно, разобрано не больше семи стекол, значит хотя бы одно из восьми стекол, предназначавшихся заранее для восьми оставшихся окон, осталось. Его-то и можно вставить в «свое" окно. Поэтому больше семи окон остаться незастекленными не может.
Теперь покажем, что семь окон могут остаться незастекленными. Это произойдет, например, в следующем случае. Стекла имеют такие размеры, что для любых двух одно может быть получено из другого вырезанием (заметим, что условие задачи этого не требует). Таким образом, все стекла можно упорядочить от самого маленького до самого большого так, что любое меньшее может быть «вырезано" из большего. Соответствующим образом упорядочиваются и окна. Предположим, стекольщик подходит к окнам в порядке возрастания их размера (от самого маленького к самому большому), а стекла подбирает в порядке убывания размера. При этом ему удастся застеклить 8 самых маленьких окон, восьмое окно получит «свое" стекло. Останутся незастекленными 7 самых больших окон и неиспользованными 7 самых маленьких стекол.
Задача 6: (7–8) Из бумаги склеено цилиндрическое кольцо, ширина которого равна 1, а длина по окружности равна 4. Можно ли не разрывая сложить это кольцо так, чтобы получился квадрат площади 2? Решение: Отметим на одной кромке кольца диаметрально противоположные точки A и C, а на другой — диаметрально противоположные точки B и D, повернутые относительно A и C на 90. На рис. 10,а) изображен прямоугольник, получаемый из кольца разрезанием по образующей цилиндра
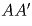 . Сложив цилиндр по линиям AB, BC, CD и
DA, получим квадрат площади 2 (рис. 10,б).
. Сложив цилиндр по линиям AB, BC, CD и
DA, получим квадрат площади 2 (рис. 10,б).Задача 7: (9) Точка M внутри выпуклого четырехугольника ABCD такова, что площади треугольников ABM, BCM, CDM и DAM равны. Верно ли, что ABCD — параллелограмм, а точка M — точка пересечения его диагоналей? Решение: Это утверждение неверно. Рассмотрим произвольный треугольник ABC, у которого
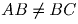 и симметричный ему
треугольник ADC относительно прямой AC. Середину общей
стороны AC этих треугольников обозначим M. Из того, что
медиана делит треугольник на две равновеликие части следует, что
четырехугольник ABCD и точка M будут искомыми.
и симметричный ему
треугольник ADC относительно прямой AC. Середину общей
стороны AC этих треугольников обозначим M. Из того, что
медиана делит треугольник на две равновеликие части следует, что
четырехугольник ABCD и точка M будут искомыми.Задача 8: (9) В каждый узел бесконечной клетчатой бумаги воткнута вертикальная булавка. Иголка длины l лежит на бумаге параллельно линиям сетки. При каких l иголку можно повернуть на 90, не выводя из плоскости бумаги? Иголку разрешается как угодно двигать по плоскости, но так, чтобы она проходила между булавками; толщиной булавок и иголки пренебречь.
Решение: Соединим отрезками всевозможные пары узлов клетчатой бумаги, расстояние между которыми не превосходит l. Будем считать, что один из концов O иголки не лежит ни на одном из нарисованных отрезков (в противном случае этого можно добиться небольшим шевелением иголки). Начнем поворачивать иголку вокруг этого конца. Если в процессе этого движения она упрется в булавку, то станем двигать иголку вдоль себя до тех пор, пока она не перестанет соприкасаться с булавкой (при таком движении мы можем быть уверены, что не упремся ни в какую другую булавку, в силу выбора начального положения конца иголки). Затем будем двигать иголку вдоль себя в обратном направлении (но оставляя булавку на сей раз с другой стороны от иголки) до тех пор, пока ее конец O не вернется в исходное положение. Продолжая действовать таким образом, мы сможем повернуть иголку на любой угол.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1982 | Убрать решения |