Задача 1:
(5–7)
В поход пошли 20 туристов. Самому старшему из них 35 лет,
а самому младшему 20 лет. Верно ли, что среди туристов есть
одногодки?
Задача 2:
(5–9)
На столе стоят 16 стаканов. Из них 15 стаканов стоят
правильно, а один перевернут донышком вверх. Разрешается
одновременно переворачивать любые четыре стакана. Можно ли,
повторяя эту операцию, поставить все стаканы правильно?
Задача 3:
(5–7)
Придя в тир, Петя купил 5 пуль. За каждый успешный
выстрел ему дают еще 5 пуль. Петя утверждает, что он сделал 50
выстрелов и 8 раз попал в цель, а его друг Вася говорит, что
этого не может быть. Кто из мальчиков прав?
Задача 4:
(5–7)
Какое наименьшее число карточек спортлото (6 из 49) надо
купить, чтобы наверняка хоть в одной из них был угадан хоть один
номер?
Задача 5:
(5–7)
Два гроссмейстера по очереди ставят на шахматную доску
ладьи (за один ход — одну ладью) так, чтобы они не били друг
друга. Тот, кто не сможет поставить ладью, проигрывает. Кто
выигрывает при правильной игре — первый или второй гроссмейстер?
Задача 6:
(5)
Дано 25 чисел. Сумма любых четырех из них положительна.
Докажите, что сумма их всех тоже положительна.
Задача 7:
(6–9)
Петя и Вася выписывают 12-значное число, ставя цифры по
очереди, начиная со старшего разряда. Начинает Вася. Докажите,
что какие бы цифры он не писал, Петя всегда сможет добиться,
чтобы получившееся число делилось на 9.
Задача 8:
(6–7)
Четыре дома расположены по окружности. Где надо вырыть
колодец, чтобы сумма расстояний от домов до колодца была
наименьшей?
Задача 9:
(6–7)
Известно, что число
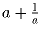
— целое.
Докажите, что число
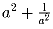
— тоже
целое.
Задача 10:
(8–9)
В турнире по олимпийской системе (проигравший выбывает)
участвует 50 боксеров. Какое наименьшее количество боев надо
провести, чтобы выявить победителя?
Задача 11:
(8–9)
Вершины одного параллелограмма лежат на сторонах другого
— по одной вершине на каждой стороне. Докажите, что центры этих
параллелограммов совпадают.
Задача 12:
(8–9)
Было 7 ящиков. В некоторые из них положили еще по 7
ящиков и т. д. В итоге стало 10 непустых ящиков. Сколько всего
стало ящиков?
Задача 13:
(8–9)
Передние покрышки автомобиля «Антилопа Гну" выходят из
строя через 25000,км, а задние — через 15000,км. Когда О.Бендер
должен поменять их местами, чтобы машина прошла максимальное
расстояние? Чему равно это расстояние ?
Задача 14:
(8–9)
Найдите наибольшее отношение трехзначного числа к
сумме его цифр.
Задача 15:
(8–9)
В классе каждый мальчик дружит ровно с двумя
девочками, а каждая девочка — ровно с тремя мальчиками. Еще
известно, что в классе 31 пионер и 19 парт. Сколько человек в этом
классе?
Задача 16:
(8–9)
Каждый из четырех гномов — Беня, Веня, Женя,
Сеня — либо всегда говорит правду, либо всегда врет. Мы услышали
такой разговор: Беня — Вене: «ты врун"; Женя — Бене: «сам ты
врун"; Сеня — Жене: «да оба они вруны, — (подумав), —
впрочем, ты тоже". Кто из них говорит правду?
Задача 17:
(8–9)
В классе 25 человек. Известно, что среди любых
трех из них есть двое друзей. Докажите, что есть ученик, у
которого не менее 12 друзей.
Задача 18:
(8–9)
Между соседними лагерями 1 день пути. Экспедиции
требуется перенести 1 банку консервов в лагерь, находящийся в
5 днях пути от базового и вернуться обратно. При этом:
— каждый член экспедиции может нести с собой не более 3 банок
консервов;
— за 1 день он съедает 1 банку консервов;
— оставлять консервы можно только в лагерях.
Какое наименьшее количество банок консервов придется взять из
базового лагеря для этой цели?


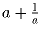 — целое.
Докажите, что число
— целое.
Докажите, что число 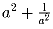 — тоже
целое.
Задача 10:
(8–9)
В турнире по олимпийской системе (проигравший выбывает)
участвует 50 боксеров. Какое наименьшее количество боев надо
провести, чтобы выявить победителя?
Задача 11:
(8–9)
Вершины одного параллелограмма лежат на сторонах другого
— по одной вершине на каждой стороне. Докажите, что центры этих
параллелограммов совпадают.
Задача 12:
(8–9)
Было 7 ящиков. В некоторые из них положили еще по 7
ящиков и т. д. В итоге стало 10 непустых ящиков. Сколько всего
стало ящиков?
Задача 13:
(8–9)
Передние покрышки автомобиля «Антилопа Гну" выходят из
строя через 25000,км, а задние — через 15000,км. Когда О.Бендер
должен поменять их местами, чтобы машина прошла максимальное
расстояние? Чему равно это расстояние ?
— тоже
целое.
Задача 10:
(8–9)
В турнире по олимпийской системе (проигравший выбывает)
участвует 50 боксеров. Какое наименьшее количество боев надо
провести, чтобы выявить победителя?
Задача 11:
(8–9)
Вершины одного параллелограмма лежат на сторонах другого
— по одной вершине на каждой стороне. Докажите, что центры этих
параллелограммов совпадают.
Задача 12:
(8–9)
Было 7 ящиков. В некоторые из них положили еще по 7
ящиков и т. д. В итоге стало 10 непустых ящиков. Сколько всего
стало ящиков?
Задача 13:
(8–9)
Передние покрышки автомобиля «Антилопа Гну" выходят из
строя через 25000,км, а задние — через 15000,км. Когда О.Бендер
должен поменять их местами, чтобы машина прошла максимальное
расстояние? Чему равно это расстояние ?