 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1985 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1985 |
|
|
Задача 2: (5–9) На столе стоят 16 стаканов. Из них 15 стаканов стоят правильно, а один перевернут донышком вверх. Разрешается одновременно переворачивать любые четыре стакана. Можно ли, повторяя эту операцию, поставить все стаканы правильно? Решение: Посмотрим, как изменяется количество правильно стоящих стаканов при каждой такой операции. Очевидно, что это зависит от того, сколько из переворачиваемых стаканов стоят правильно, а сколько — вверх дном. А именно: — если все четыре переворачиваемых стакана стоят правильно, то количество правильно стоящих стаканов уменьшится на 4; — если из четырех стаканов правильно стоят три, то это количество уменьшится на 2; — если два, то количество не изменится; — если один, то увеличится на 2; — если все переворачиваемые стаканы стояли вверх дном, то количество правильно стоящих стаканов увеличится на 4.
В любом случае количество правильно стоящих стаканов либо остается прежним, либо изменяется на четное число. Поскольку сначала таких стаканов 15, то и в любой момент их будет нечетное количество. Поэтому добиться того, чтобы 16 стаканов стояли правильно, нельзя.
Задача 3: (5–7) Придя в тир, Петя купил 5 пуль. За каждый успешный выстрел ему дают еще 5 пуль. Петя утверждает, что он сделал 50 выстрелов и 8 раз попал в цель, а его друг Вася говорит, что этого не может быть. Кто из мальчиков прав? Решение: Если Петя купил вначале 5 пуль, а всего сделал 50 выстрелов, то 45 пуль он получил за успешные выстрелы. Но для этого ему надо было попасть в цель 9 раз. А он утверждает, что сделал только 8 метких выстрелов. Значит, он не прав.
Задача 4: (5–7) Какое наименьшее число карточек спортлото (6 из 49) надо купить, чтобы наверняка хоть в одной из них был угадан хоть один номер? Решение: Покажем, что восьми карточек достаточно. Заполним их следующим образом: в первой зачеркнем числа от 1 до 6, во второй — от 7 до 12 и т. д., в последней — от 43 до 48. Не зачеркнутым ни в одной карточке останется только число 49. Поэтому среди выигрышных номеров по крайней мере пять окажутся зачеркнутыми (к сожалению, нельзя гарантировать, что эти пять номеров будут зачеркнуты в одной карточке).
Теперь нам нужно доказать, что семи карточек может не хватить. Действительно, всего будет вычеркнуто не более 42 различных чисел. Поэтому не менее семи чисел окажутся не вычеркнутыми ни в одной из карточек. Может так случиться, что выигрышными окажутся как раз шесть чисел из этих семи.
Задача 5: (5–7) Два гроссмейстера по очереди ставят на шахматную доску ладьи (за один ход — одну ладью) так, чтобы они не били друг друга. Тот, кто не сможет поставить ладью, проигрывает. Кто выигрывает при правильной игре — первый или второй гроссмейстер? Решение: Вспомним, что поля шахматной доски можно задавать координатами — буквой от a до h, обозначающей вертикаль, и цифрой от 1 до 8, обозначающей горизонталь. Очевидно, что поставить ладью на некоторое поле можно тогда и только тогда, когда ни на горизонтали, ни на вертикали, содержащей это поле, не стоит ладьи. Поэтому описанная выше игра равносильна следующей: гроссмейстеры по очереди вычеркивают из набора букв a,b, … ,h и цифр 1,2, … ,8 по одной букве и цифре. Очевидно, что как бы ни ходили игроки, после восьмого хода все буквы и цифры будут вычеркнуты. Восьмой ход принадлежит второму, поэтому первый не сможет сделать следующего хода. Заметим «необычность" этой игры: второй игрок выигрывает независимо от того, как будут играть он и его соперник.
Задача 6: (5) Дано 25 чисел. Сумма любых четырех из них положительна. Докажите, что сумма их всех тоже положительна. Решение: Среди данных чисел должно быть хотя бы одно положительное. Действительно, возьмем любые четыре из этих чисел. Если бы все они были неположительны, то и их сумма была бы неположительной, что противоречит условию. (На самом деле, таким образом доказывается более сильное утверждение — что положительных чисел в данном наборе не меньше 22, однако нам понадобится существование лишь одного такого числа.) Выберем это положительное число. Остальные 24 числа разобьем произвольным образом на шесть четверок. Сумма всех 25 чисел — это сумма выбранного числа (которое положительно по выбору) и сумм получившихся четверок (которые положительны по условию). Она является положительной.
Задача 7: (6–9) Петя и Вася выписывают 12-значное число, ставя цифры по очереди, начиная со старшего разряда. Начинает Вася. Докажите, что какие бы цифры он не писал, Петя всегда сможет добиться, чтобы получившееся число делилось на 9. Решение: Число делится на 9, если сумма его цифр делится на 9 (См. Т8). Поэтому одна из возможных стратегий для Пети — дополнять на каждом ходу Васину цифру до 9. То есть, если Вася пишет «0", то Петя пишет «9", если Вася пишет «1", то Петя пишет «8" и т.д. Таким образом, после каждой пары ходов Васи и Пети сумма цифр будет увеличиваться на 9. К моменту написания всего числа она станет равной
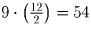 .
.Заметим, что указанная стратегия не единственна. Попробуйте доказать, что независимо от того, какие цифры будут стоять перед последним ходом Пети в одиннадцати разрядах, своим последним ходом Петя сможет добиться, чтобы число делилось на 9. То есть все цифры кроме последней Петя может ставить произвольно!
Задача 8: (6–7) Четыре дома расположены по окружности. Где надо вырыть колодец, чтобы сумма расстояний от домов до колодца была наименьшей? Решение: Обозначим дома буквами A, B, C, D в порядке их следования по окружности. Предположим, колодец вырыт в точке O. Из неравенства треугольника (см. Т17) следует, что OA + OC ≥ AC, причем равенство достигается тогда и только тогда, когда точка O принадлежит отрезку AC. Аналогично, OB + OD ≥ BD, причем равенство имеет место тогда и только тогда, когда O лежит на отрезке BD. Складывая эти неравенства, получим: OA + OB + OC + OD ≥ AC + BD. Равенство выполняется только тогда, когда O — точка пересечения отрезков AC и BD.
Поэтому колодец нужно вырыть в точке пересечения диагоналей четырехугольника ABCD.
Задача 9: (6–7) Известно, что число
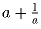 — целое.
Докажите, что число
— целое.
Докажите, что число 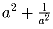 — тоже
целое.
Решение:
Доказательство следует из формулы:
— тоже
целое.
Решение:
Доказательство следует из формулы:
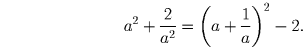
Задача 10: (8–9) В турнире по олимпийской системе (проигравший выбывает) участвует 50 боксеров. Какое наименьшее количество боев надо провести, чтобы выявить победителя? Решение: После каждого боя из соревнований выбывает один боксер — проигравший в этом бою. Поскольку всего к концу соревнований выбыть должны все, кроме победителя, всего должно быть 49 боев, независимо от того, как составляется расписание.
Задача 11: (8–9) Вершины одного параллелограмма лежат на сторонах другого — по одной вершине на каждой стороне. Докажите, что центры этих параллелограммов совпадают. Решение: Пусть A, B, C, D — вершины одного параллелограмма, лежащие на сторонах a, b, c, d другого параллелограмма соответственно (рис. 14). Пусть O — центр параллелограмма ABCD. При симметрии относительно точки O точки A и C, а также точки B и D попарно переходят друг в друга. Прямая a переходит в параллельную ей прямую, проходящую через точку C — образ точки A, то есть в прямую c. Аналогично, прямая b переходит в прямую d. Значит, «внешний" параллелограмм при этой симметрии переходит в себя, то есть точка O является его центром.
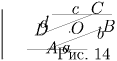
Задача 12: (8–9) Было 7 ящиков. В некоторые из них положили еще по 7 ящиков и т. д. В итоге стало 10 непустых ящиков. Сколько всего стало ящиков? Решение: При каждой операции заполняется один пустой ящик. Поскольку стало 10 непустых ящиков, то было проведено 10 операций. Вначале было 7 ящиков, и при каждой операции добавлялось еще по 7. Поэтому в результате стало 77 ящиков.
Задача 13: (8–9) Передние покрышки автомобиля «Антилопа Гну" выходят из строя через 25000,км, а задние — через 15000,км. Когда О.Бендер должен поменять их местами, чтобы машина прошла максимальное расстояние? Чему равно это расстояние ?
Решение: Каждый километр пробега передних покрышек изнашивает их на
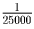 ,, а задних — на
,, а задних — на
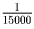 ,. Поэтому если в середине пути длиной
L,км покрышки поменять, то их износ за весь путь будет равен
,. Поэтому если в середине пути длиной
L,км покрышки поменять, то их износ за весь путь будет равен
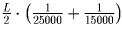 .
Приравняв эту величину единице, мы получим путь, который можно
пройти до полного износа покрышек. Он равен
.
Приравняв эту величину единице, мы получим путь, который можно
пройти до полного износа покрышек. Он равен
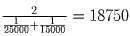 ,(км).
,(км).Очевидно, что сменить покрышки в середине пути — оптимальная стратегия, так как если это сделать в другом месте, то покрышки, прошедшие сзади больше, чем впереди, выйдут из строя раньше. Значит, поменять покрышки надо через 9375,км пути.
Задача 14: (8–9) Найдите наибольшее отношение трехзначного числа к сумме его цифр. Решение:
Рассмотрим произвольное трехзначное число
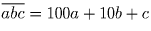 и его отношение к своей сумме цифр.
Имеем
и его отношение к своей сумме цифр.
Имеем
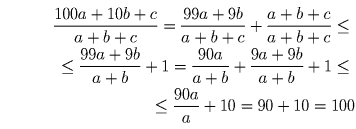
В первом из двух неравенств равенство выполняется при c = 0, а во втором — при b = 0. Поэтому искомое наибольшее равно 100 и достигается для трехзначных чисел, записи которых оканчиваются двумя нулями.
Задача 15: (8–9) В классе каждый мальчик дружит ровно с двумя девочками, а каждая девочка — ровно с тремя мальчиками. Еще известно, что в классе 31 пионер и 19 парт. Сколько человек в этом классе? Решение:
Обозначим количество мальчиков в классе через M, а девочек —
через D. Из условий следует, что 31 ≤ D + M ≤ 38 и 3D = 2M.
Последнее равенство показывает, что количество девочек четно, а
количество мальчиков делится на 3. Более того,
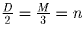 , откуда D + M = 5n.
Существует единственное целое число, заключенное между 31 и 38,
делящееся на 5. Поэтому можно утверждать, что в классе 35 учеников
— 14 девочек и 21 мальчик.
, откуда D + M = 5n.
Существует единственное целое число, заключенное между 31 и 38,
делящееся на 5. Поэтому можно утверждать, что в классе 35 учеников
— 14 девочек и 21 мальчик.
Задача 16: (8–9) Каждый из четырех гномов — Беня, Веня, Женя, Сеня — либо всегда говорит правду, либо всегда врет. Мы услышали такой разговор: Беня — Вене: «ты врун"; Женя — Бене: «сам ты врун"; Сеня — Жене: «да оба они вруны, — (подумав), — впрочем, ты тоже". Кто из них говорит правду? Решение:
Предположим, Сеня говорит правду. Тогда, согласно его словам, три остальных гнома — вруны. И, тем самым, фраза Бени является правдой. Значит, предположение приводит к противоречию, поэтому Сеня — врун, и его утверждение, что Женя — врун, является ложным. Отсюда заключаем, что Женя говорит правду. Тем самым, Беня — врун, а Веня говорит правду. Отметим, что фраза Сени «да оба они вруны" (относительно Бени и Вени) является ложной (несмотря на то, что Беня действительно врун), поскольку Веня — не врун.
Задача 17: (8–9) В классе 25 человек. Известно, что среди любых трех из них есть двое друзей. Докажите, что есть ученик, у которого не менее 12 друзей. Решение:
Рассмотрим двоих учеников класса, которые не дружат между собой. (Если таких нет, то все ученики класса дружат между собой, значит, у каждого ученика имеется 24 друга, и задача решена.) Пусть этими двумя будут Вася и Петя. Тогда из оставшихся 23 учеников каждый дружит либо с Васей, либо с Петей. Действительно, если бы кто-то (скажем, Коля) не дружил бы ни с Васей, ни с Петей, то мы имели бы троих учеников, среди которых не было бы друзей. Теперь если предположить, что и Вася, и Петя имеют не более 11 друзей, то всего в классе, кроме этих двоих было бы не больше 22 человек (см. Т2). Полученное противоречие показывает, что один из школьников имеет не менее 12 друзей.
Задача 18: (8–9) Между соседними лагерями 1 день пути. Экспедиции требуется перенести 1 банку консервов в лагерь, находящийся в 5 днях пути от базового и вернуться обратно. При этом: — каждый член экспедиции может нести с собой не более 3 банок консервов; — за 1 день он съедает 1 банку консервов; — оставлять консервы можно только в лагерях. Какое наименьшее количество банок консервов придется взять из базового лагеря для этой цели? Решение:
Предположим, что в каждом лагере имеется торговая палатка, где продаются доставленные консервы. Пусть цена одной банки в базовом лагере равна одному рублю, а в каждом следующем — в три раза больше, чем в предыдущем. В таком случае цена банок, доставленных в любой из лагерей не меньше, чем цена банок, взятых для этого из базового лагеря. Действительно, для переноски банки из некоторого лагеря в следующий мы должны взять по крайней мере три банки, две из которых будут съедены на пути туда и обратно соответственно. Стоимость банки в пятом лагере будет при этом 35 = 243,руб., значит из базового лагеря нужно взять не менее 243 банок.
Докажем теперь, что 243 банок хватит. Для этого из базового лагеря выходит 81 член экспедиции. 54 человека из них, принеся по банке в первый лагерь, сразу возвращаются. Остальные 27 человек, взяв по три банки, идут во второй лагерь. 27 банок при этом остаются в первом лагере, чтобы обеспечить им возвращение из первого лагеря в базовый. Так происходит в каждом лагере. Две трети дошедших участников возвращаются, а треть — идет дальше. Таким образом, из четвертого лагеря в пятый выйдет один человек. Он и принесет вожделенную банку в пятый лагерь.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1985 | Убрать решения |