Задача 1: (5–7) Вычислить

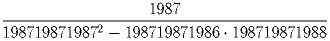
Задача 2: (5–7) Найти все числа, которые в 12 раз больше суммы своих цифр.

Задача 3: (5–7) Али-Баба пришел в пещеру, где есть золото, алмазы и сундук, в котором их можно унести. Полный сундук золота весит 200,кг, полный сундук алмазов — 40,кг, пустой сундук ничего не весит. Килограмм золота стоит на базаре 20 динаров, килограмм алмазов — 60 динаров. Али-Баба может поднять и унести не более 100,кг. Сколько денег он может получить за сокровища, которые он принесет из пещеры за один раз?

Задача 4: (8–9) На плоскости даны четыре точки, не лежащие на одной прямой. Докажите, что существует неостроугольный треугольник с вершинами в этих точках.

Задача 5: (8–9) Пусть a и b — целые числа. Докажите, что если a² + 9ab + b² делится на 11, то и a² – b² делится на 11.

Задача 6: (8–9) На окружности даны 10 точек. Сколькими способами можно провести пять отрезков, не имеющих общих точек, с концами в данных точках?

Задача 7: (8–9) Брат и сестра делят треугольный торт так: он указывает точку на торте, а она проводит через эту точку прямолинейный разрез и выбирает себе кусок. Каждый хочет получить кусок как можно больше. Где брат должен поставить точку? Какую часть торта получит в этом случае каждый из них?

Задача 8: (5–7) a, b, c, d — стороны четырехугольника четырехугольника, S — сумма длин его диагоналей. Докажите, что:

а) S < P;

б) P < 2S.

Задача 9: (5–7) В центре квадратного пруда плавает ученик. Внезапно к вершине квадрата подошел учитель. Учитель не умеет плавать, но ходит в 4 раза быстрее, чем ученик плавает. Ученик бегает быстрее. Сможет ли он убежать?

Задача 10: (5–7) Компьютер может производить одну операцию: брать среднее арифметическое двух целых чисел. Даны три числа: m, n и 0, причем m и n не имеют общих делителей и m < n. Докажите, что с помощью компьютера из них можно получить

а) единицу;

б) любое целое число от 1 до n.

Задача 11: (5–7) Шалтай-Болтай ходит по прямой, проходя за минуту либо на 37 шагов влево, либо на 47 шагов вправо. За какое наименьшее время он может оказаться на один шаг правее исходной точки?

Задача 12: (8–9) Известно, что некоторый многочлен в рациональных точках принимает рациональные значения. Докажите, что все его коэффициенты рациональные.

Задача 13: (8–9) Какое максимальное число ладей можно расставить в кубе 8 × 8 × 8, чтобы они не били друг друга?

Задача 14: (8–9) Докажите, что существует число, сумма цифр квадрата которого более, чем в 1000 раз превышает сумму цифр самого числа.

Задача 15: (8–9) Дан выпуклый пятиугольник. Каждая диагональ отсекает от него треугольник. Докажите, что сумма площадей треугольников больше площади пятиугольника.