 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1987 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1987 |
|
|
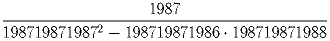
Задача 2: (5–7) Найти все числа, которые в 12 раз больше суммы своих цифр. Решение: Пусть искомое число содержит n цифр. Тогда оно не меньше, чем 10n – 1 (это наименьшее n-значное число). С другой стороны, сумма его цифр не больше 9n (так как каждая цифра не больше 9). Поэтому из условия задачи следует, что искомое число не больше, чем 12 • 9n. Докажем по индукции (см. Т1), что при n ≥ 4 имеет место неравенство 10n – 1 > 108n; При n = 4 неравенство имеет вид 1000 > 432, что, очевидно, справедливо. Пусть оно справедливо при n = k. Это значит, что 10k – 1 > 108k. Умножив это неравенство на верное неравенство
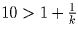 (см. Т13), получим
(см. Т13), получим
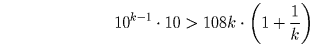
Из сказанного выше следует, что искомое число является двузначным или трехзначным (однозначным оно, очевидно, быть не может, так как сумма цифр однозначного числа всегда равна ему самому). Рассмотрим эти два случая.
Первый случай: n = 2. Пусть искомое число записывается цифрами a и b. Это значит, что оно равно 10a + b, и условие задачи запишется в виде 10a + b = 12 • (a + b), откуда 2a + 11b = 0, что невозможно.
Второй случай: n = 3. Пусть искомое число записывается цифрами a, b и c. В этом случае условие задачи записывается в виде уравнения 100a + 10b + c = 12(a + b + c), откуда 88a = 2b + 11c, и 11(8a – c) = 2b. Мы получили, что 2b делится на 11. Вспомнив, что 0 ≤ b ≤ 9, получаем единственно возможный случай: b = 0. Далее, 8a = c. Здесь опять все однозначно: a = 1, c = 8. Итак, 108 — единственное число, удовлетворяющее условиям задачи.
Задача 3: (5–7) Али-Баба пришел в пещеру, где есть золото, алмазы и сундук, в котором их можно унести. Полный сундук золота весит 200,кг, полный сундук алмазов — 40,кг, пустой сундук ничего не весит. Килограмм золота стоит на базаре 20 динаров, килограмм алмазов — 60 динаров. Али-Баба может поднять и унести не более 100,кг. Сколько денег он может получить за сокровища, которые он принесет из пещеры за один раз? Решение: Предположим, что Али-Баба смог унести из пещеры x,кг золота и y,кг алмазов. В этом случае он сможет получить 20x + 60y динаров. Поскольку Али-Баба может поднять не более 100,кг, то
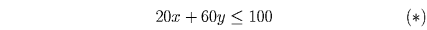
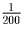 часть
сундука, а 1,кг алмазов занимает
часть
сундука, а 1,кг алмазов занимает 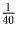 часть
сундука. Значит, взятые Али-Бабой сокровища займут
часть
сундука. Значит, взятые Али-Бабой сокровища займут
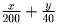 часть
сундука. В распоряжении Али-Бабы только один сундук, поэтому
получаем новое ограничение на количество взятого им сокровища:
часть
сундука. В распоряжении Али-Бабы только один сундук, поэтому
получаем новое ограничение на количество взятого им сокровища:

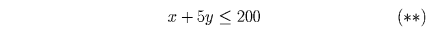
Осталось показать, что Али-Баба сможет унести сокровища на 3000 динаров. Для этого, очевидно, необходимо и достаточно чтобы в неравенствах (*) и (**) были выполнены равенства. Решив соответствующую систему двух уравнений, найдем x = 75, y = 25.
Итак, Али-Баба сможет получить 3000 динаров, взяв из пещеры 75,кг золота и 25,кг алмазов.
Задача 4: (8–9) На плоскости даны четыре точки, не лежащие на одной прямой. Докажите, что существует неостроугольный треугольник с вершинами в этих точках. Решение: Рассмотрим отдельно различные случаи расположения четырех данных точек на плоскости (см. Т16).
Пусть четыре данные точки являются вершинами выпуклого четырехугольника. Известно, что сумма углов выпуклого четырехугольника равна 360. Поэтому хотя бы один из его углов не острый. Действительно, если бы все его углы имели величину меньше 90, то сумма его углов была бы меньше 4 • 90 = 360. Обозначим вершину четырехугольника, угол при которой не острый, через A. Тогда треугольник с вершинами в точке A и двух соседних с ней вершинах четырехугольника будет неостроугольным (рис. 24,а).
Предположим теперь, что одна из точек (обозначим ее A) лежит внутри треугольника BCD, образованного остальными тремя точками (рис. 24,б). Сумма углов BAC, CAD и DAB равна 360. Поэтому по крайней мере один из них имеет величину не меньше 120. Неостроугольный треугольник найден и в этом случае.
Наконец, рассмотрим случай когда три точки лежат на одной прямой. Обозначим эти точки A, B и C в порядке их следования на прямой, четвертую точку обозначим D (рис. 24,в). Тогда сумма углов DBA и DBC равна 180. Значит, один из этих углов больше 90. В этом случае требуемый треугольник тоже найден.
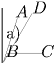
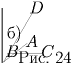
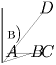
Задача 6: (8–9) На окружности даны 10 точек. Сколькими способами можно провести пять отрезков, не имеющих общих точек, с концами в данных точках? Решение: Обозначим через Cn количество способов, которыми можно соединить 2n точек на окружности n отрезками, не имеющими общих точек. В задаче требуется найти C5. Очевидно, что C1 = 1. Будем считать также, что C0 = 1. Докажем следующую формулу
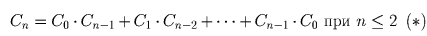
Для этого рассмотрим окружность с отмеченными на ней 2n точками. Обозначим одну из них через A. Она должна быть соединена с некоторой другой точкой. Подсчитаем, сколькими способами можно соединить остальные точки, если точка A уже соединена с некоторой точкой B. Остальные 2n – 2 точки делятся прямой AB на две группы, лежащие по разные стороны от этой прямой. Для того, чтобы удовлетворить условиям задачи, точки каждой из этих частей можно соединять только между собой, так как отрезок их соединяющий пересекает отрезок AB. В частности, удовлетворить условиям задачи можно только если количество точек с каждой стороны от отрезка AB является четным. Если с одной стороны от прямой AB находится 2k точек, то количество способов их соединить равно Ck. При этом с другой стороны от прямой AB будет находится 2(n – k – 1) точек, и количество способов соединить их между собой равно Cn – k – 1. При каждом способе соединения точек, лежащих с одной стороны от AB, можно осуществить все способы соединения точек, лежащих с другой стороны от AB. Поэтому общее число способов соединения равно произведению Ck • Cn – k – 1. Для того, чтобы получить Cn, мы должны просуммировать эту величину для всех возможных точек B. При этом число k будет, очевидно, пробегать все значения от нуля до n – 1. В результате получим формулу (*).
Пользуясь формулой (*), получаем C2 = C0 • C1 + C1 • C0 = 1 • 1 + 1 • 1 = 2 C3 = C0 • C2 + C1 • C1 + C2 • C0 = 1 • 2 + 1 • 1 + 2 • 1 = 5 C4 = C0 • C3 + C1 • C2 + C2 • C1 + C3 • C0 = = 1 • 5 + 1 • 2 + 2 • 1 + 5 • 1 = 14 C5 = C0 • C4 + C1 • C3 + C2 • C2 + C3 • C1 + C4 • C0 = 1 • 14 + 1 • 5 + 2 • 2 + 5 • 1 + 14 • 1 = 42
Задача 7: (8–9) Брат и сестра делят треугольный торт так: он указывает точку на торте, а она проводит через эту точку прямолинейный разрез и выбирает себе кусок. Каждый хочет получить кусок как можно больше. Где брат должен поставить точку? Какую часть торта получит в этом случае каждый из них? Решение: Докажем сначала следующую лемму.
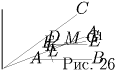
Лемма. Пусть ABC — произвольный треугольник, M — его точка пересечения медиан. Тогда
а) прямая, параллельная стороне треугольника и проходящая через точку M, разбивает его на треугольник и трапецию, отношение площадей которых равно 4:5;
б) любая другая прямая, проходящая через точку M, разбивает его на части, отношение площадей которых больше 4:5.
Пусть прямая l, параллельная стороне AB, пересекает сторону
AC в точке D, а сторону BC — в точке E (рис. 25).
Треугольники DEC и ABC подобны (по двум углам). Коэффициент
k подобия равен 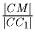 , где |CC1|
— медиана треугольника ABC. Поскольку медианы в точке
пересечения делятся в отношении 2:1, то k = ⅔.
Отношение площадей подобных треугольников равно квадрату
коэффициентов подобия. Поэтому
, где |CC1|
— медиана треугольника ABC. Поскольку медианы в точке
пересечения делятся в отношении 2:1, то k = ⅔.
Отношение площадей подобных треугольников равно квадрату
коэффициентов подобия. Поэтому
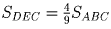 , соответственно,
, соответственно,
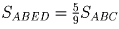 .
Утверждение а) леммы доказано.
.
Утверждение а) леммы доказано.
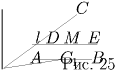
Известно, что медиана делит треугольник на два треугольника равной площади. Действительно, у этих треугольников равные основания и общая высота. Поэтому если рассматриваемая прямая проходит через вершину треугольника, то отношение площадей частей, на которые она делит треугольник, равно 1, и утверждение б) в этом случае справедливо.
Проведем теперь через точку M прямую FG, находящуюся в «промежуточном положении" между прямой DE, параллельной стороне AB, и прямой AA1, содержащей медиану треугольника (рис. 25). Докажем, что
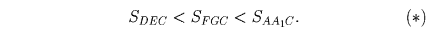
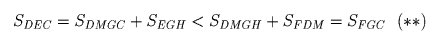
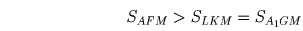
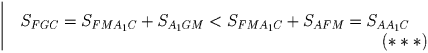
Рассмотренный случай расположения прямой, делящей треугольник, является общим. Лемма доказана.
Перейдем теперь непосредственно к задаче о разрезании торта.
Из доказанной леммы следует, что если брат укажет на торте точку
пересечения медиан, то тем самым добьется, что сестра получит не
более 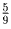 торта.
торта.
Докажем теперь, что независимо от того, какую точку он укажет на
торте, она сможет отрезать себе не менее 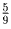 торта. Проведем для этого через точку O, указанную братом, три
прямые, параллельные сторонам треугольника (рис. 27). Каждая из
них разбивает треугольник на треугольник и трапецию. Три
полученные трапеции целиком покрывают исходный торт-треугольник.
Поэтому по крайней мере одна из них содержит его точку пересечения
медиан. Из леммы легко вывести, что площадь этой трапеции не меньше
торта. Проведем для этого через точку O, указанную братом, три
прямые, параллельные сторонам треугольника (рис. 27). Каждая из
них разбивает треугольник на треугольник и трапецию. Три
полученные трапеции целиком покрывают исходный торт-треугольник.
Поэтому по крайней мере одна из них содержит его точку пересечения
медиан. Из леммы легко вывести, что площадь этой трапеции не меньше
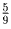 площади всего торта. Эту трапецию она и
должна отрезать для себя.
площади всего торта. Эту трапецию она и
должна отрезать для себя.
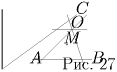
Задача 8: (5–7) a, b, c, d — стороны четырехугольника четырехугольника, S — сумма длин его диагоналей. Докажите, что:
а) S < P;
б) P < 2S.
Решение:Пусть ABCD — данный четырехугольник, O — точка пересечения его диагоналей.
а) Запишем неравенство треугольника (см. Т17) для треугольников AOB, BOC, COD и DOA:
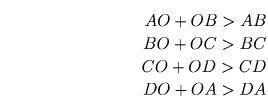
(неравенства строгие, поскольку точка O не лежит ни на одной из сторон четырехугольника ABCD). Сложив эти неравенства и воспользовавшись тем, что AO + OC = BO + OD = S, получим требуемое.
б) Запишем неравенство треугольника для ABC, BCD, CDA и DAB:
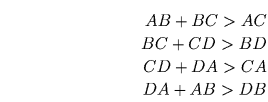
(опять же, все неравенства строгие). Сложив их, получим требуемое.
Задача 9: (5–7) В центре квадратного пруда плавает ученик. Внезапно к вершине квадрата подошел учитель. Учитель не умеет плавать, но ходит в 4 раза быстрее, чем ученик плавает. Ученик бегает быстрее. Сможет ли он убежать? Решение:
Покажем, что ученик может убежать от учителя. Обозначим квадрат пруда ABCD, его центр O. Предположим, учитель подошел к вершине C. Будем обозначать положение ученика в любой момент времени точкой M, а учителя — точкой U. Пусть также M1 и M2 — проекции точки M на стороны AB и AD соответственно; U1 — точка, симметричная точке U относительно центра O пруда (рис. 28). Тогда ученик должен плыть по направлению к вершине A до тех пор, пока точка U1 остается внутри угла M1MM2. Как только точка U1 совпадет с одной из точек M1 или M2, ученик поворачивает в направлении этой точки. Чтобы доплыть до берега ему надо проплыть меньше половины длины стороны квадрата. Учителю же нужно пробежать половину периметра квадрата. Значит, путь учителя более, чем в 4 раза длиннее, чем ученика. Поэтому ученик убежит от учителя.
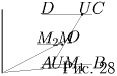
Задача 10: (5–7) Компьютер может производить одну операцию: брать среднее арифметическое двух целых чисел. Даны три числа: m, n и 0, причем m и n не имеют общих делителей и m < n. Докажите, что с помощью компьютера из них можно получить
а) единицу;
б) любое целое число от 1 до n.
Решение:Заметим, что среднее арифметическое двух целых чисел является целым тогда и только тогда, когда они одной четности (то есть оба четные или оба нечетные). Поскольку компьютер может оперировать лишь с целыми числами, то, без ограничения общности, можно считать, что разрешается брать среднее арифметическое чисел одной четности.
Будем называть множество целых чисел стабильным, если для любых двух его элементов одной четности, их среднее арифметическое также принадлежит этому множеству. Другими словами, если с помощью данного компьютера его нельзя расширить.
Разберемся, как устроены стабильные множества? Будем предполагать, что рассматриваемые множества упорядочены (по возрастанию). Заметим, что четные и нечетные числа в стабильном множестве чередуются. Действительно, если в нем имеются два соседних числа одной четности, то их среднее арифметическое является целым, лежащим между ними, что противоречит определению стабильного множества. Рассмотрим теперь произвольный (не крайний) элемент стабильного множества. Так как он имеет разную четность с обоими своими соседними элементами, то эти два элемента имеют одну четность. Их среднее арифметическое, тем самым, равно рассматриваемому числу. Если любой элемент множества является средним арифметическим соседних, то это — арифметическая прогрессия. (Мы рассматриваем как бесконечные — в одну или обе стороны — прогрессии, так и конечные). Таким образом, любое стабильное множество является арифметической прогрессией.
Итак, мы имеем три числа 0, m и n. По крайней мере два из них имеют одинаковую четность. Мы можем производить операцию взятия среднего арифметического каких-либо двух чисел и добавлять полученное число к имеющимся до тех пор, пока не получим стабильное множество. Поскольку все получаемые числа лежат в интервале от 0 до n, мы получим арифметическую прогрессию с первым членом 0, последним n и содержащим m. Поскольку m и n делятся на разность прогрессии, а по условию они взаимно просты, разность прогрессии равна 1. Значит, мы получим все числа от 0 до n.
Задача 11: (5–7) Шалтай-Болтай ходит по прямой, проходя за минуту либо на 37 шагов влево, либо на 47 шагов вправо. За какое наименьшее время он может оказаться на один шаг правее исходной точки? Решение:
Фактически, нам требуется найти решение уравнения
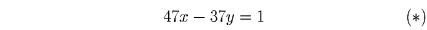
Задача 12: (8–9) Известно, что некоторый многочлен в рациональных точках принимает рациональные значения. Докажите, что все его коэффициенты рациональные. Решение:
Проведем доказательство методом математической индукции (см. Т1)
по степени многочлена. Для любого многочлена нулевой степени
(константы) утверждение очевидно. Предположим теперь, что для
многочленов степени n утверждение доказано.
Пусть P(x) = an + 1xn + 1 + anxn + … + a1x + a0
— многочлен степени n + 1, удовлетворяющий
условию задачи. Тогда по условию P(0) = a0 — свободный член
многочлена P(x) — рационален. При любом рациональном x
число
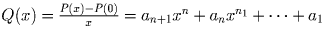 рационально.
Согласно предположению индукции, примененному к многочлену Q(x),
все его коэффициенты an + 1,an, … ,a1 рациональны.
рационально.
Согласно предположению индукции, примененному к многочлену Q(x),
все его коэффициенты an + 1,an, … ,a1 рациональны.
Задача 13: (8–9) Какое максимальное число ладей можно расставить в кубе 8 × 8 × 8, чтобы они не били друг друга? Решение:
Очевидно, что в каждом столбике из 8 кубиков-клеток может стоять только одна ладья, поэтому больше 64 ладей поставить нельзя.
Покажем, как поставить 64 ладьи, чтобы они не били друг друга. Введем систему координат с осями, направленными вдоль ребер куба так, чтобы каждая клетка имела координатами тройку (x,y,z) чисел от 0 до 7 и поставим ладьи в клетки, сумма координат которых делится на 8. Эта расстановка является искомой.
Докажем сначала, что эти ладьи не бьют друг друга. Предположим противное — какие-то две ладьи бьют друг друга. Значит, две их координаты (скажем, x и y) совпадают, а третья — различна (обозначим ее z1 и z2 соответственно). По построению суммы x + y + z1 и x + y + z2 делятся на 8. Значит, на 8 делится и их разность z1 – z2, что невозможно, так как z1 и z2 — различные неотрицательные числа, меньшие 8.
Докажем теперь, что в каждом вертикальном столбике находится по ладье, то есть что мы поставили 64 ладьи. Каждый такой столбик определяется своей парой координат x и y. Координата z для ладьи в этом столбике однозначно задается условием x + y + z ≡ 0( 8) (см. Т5). А именно, если x + y делится на 8, то z = 0, в противном случае z равно 8 минус остаток от деления на 8 суммы x + y.
Задача 14: (8–9) Докажите, что существует число, сумма цифр квадрата которого более, чем в 1000 раз превышает сумму цифр самого числа. Решение:
Таким числом будет 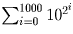 . В его
десятичной записи единицы стоят в разрядах с номерами 1, 2, 4, 8,
…, 2¹ººº (разряды мы считаем справа, то есть разряд единиц
имеет номер 1, десятков — 2 и т.д.), а остальные цифры — нули.
Сумма цифр числа равна 1001. При возведении этого числа в квадрат
мы получим единицы в разрядах с номерами 22i
(i = 0,1, … ,1000), двойки в разрядах 2i + j
(i,j = 0,1, … ,1000
. В его
десятичной записи единицы стоят в разрядах с номерами 1, 2, 4, 8,
…, 2¹ººº (разряды мы считаем справа, то есть разряд единиц
имеет номер 1, десятков — 2 и т.д.), а остальные цифры — нули.
Сумма цифр числа равна 1001. При возведении этого числа в квадрат
мы получим единицы в разрядах с номерами 22i
(i = 0,1, … ,1000), двойки в разрядах 2i + j
(i,j = 0,1, … ,1000  ) и нули в остальных местах. Сумма
цифр этого квадрата равна 1001².
) и нули в остальных местах. Сумма
цифр этого квадрата равна 1001².
Задача 15: (8–9) Дан выпуклый пятиугольник. Каждая диагональ отсекает от него треугольник. Докажите, что сумма площадей треугольников больше площади пятиугольника.
Решение:
Будем двигать вершину A данного пятиугольника ABCDE
параллельно диагонали BE. При этом площадь треугольника BEA и,
тем самым, пятиугольника ABCDE не меняется. Действительно,
основаниями всех получаемых при движении треугольников будет
отрезок BE, а высоты равны между собой. Из всех рассматриваемых
треугольников при таком движении площадь будет меняться лишь у
DEA и EAB. Как меняются эти площади? Рассмотрим один из них.
Пусть при сдвиге на
величину x точка A перейдет в точку A′ (рис. 29,a).
Обозначим через h и h′ соответственно высоты, опущенные на
сторону DE из точек A и A′ соответственно, а через 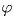 — угол между прямыми AA′ и DE. Тогда
— угол между прямыми AA′ и DE. Тогда 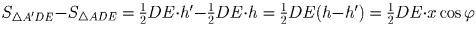 . Таким
образом, изменение площадей рассматриваемых треугольников
пропорционально величине сдвига вершины A (до тех пор, пока
какой-то из треугольников не выродится, то есть мы пересечем прямую
DE или BC). Значит, при движении в одном направлении сумма
площадей рассматриваемых треугольников возрастает, а в другом —
убывает. Без ограничения общности можно считать, что эта сумма
убывает при движении в направлении прямой DE. Значит,
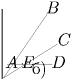
доказательство можно проводить для вырожденного пятиугольника
ABCDE, у которого вершины A, E и D лежат на одной прямой
(рис. 29,б). Рассуждая аналогично, будем двигать вершину E в
направлении вершины A или D. Таким образом мы сведем задачу к
случаю вырожденного пятиугольника, у которого две вершины (E и
A или D) совпадают. В этом случае утверждение очевидно,
поскольку уже два из рассматриваемых треугольников ABE и BCD
покрывают превратившийся в четырехугольник пятиугольник ABCDE.
. Таким
образом, изменение площадей рассматриваемых треугольников
пропорционально величине сдвига вершины A (до тех пор, пока
какой-то из треугольников не выродится, то есть мы пересечем прямую
DE или BC). Значит, при движении в одном направлении сумма
площадей рассматриваемых треугольников возрастает, а в другом —
убывает. Без ограничения общности можно считать, что эта сумма
убывает при движении в направлении прямой DE. Значит,
доказательство можно проводить для вырожденного пятиугольника
ABCDE, у которого вершины A, E и D лежат на одной прямой
(рис. 29,б). Рассуждая аналогично, будем двигать вершину E в
направлении вершины A или D. Таким образом мы сведем задачу к
случаю вырожденного пятиугольника, у которого две вершины (E и
A или D) совпадают. В этом случае утверждение очевидно,
поскольку уже два из рассматриваемых треугольников ABE и BCD
покрывают превратившийся в четырехугольник пятиугольник ABCDE.
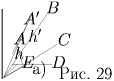
Дадим кратко другое доказательство. Назовем дефектом выпуклого пятиугольника разность между его площадью и суммой площадей треугольников, отсекаемых от него диагоналями. Мы должны доказать, что дефект любого выпуклого пятиугольника отрицателен. Из определения следует, что дефект пятиугольника меньше его площади. Для любого выпуклого пятиугольника можно рассмотреть пятиугольник, высекаемый его диагоналями. Площадь этого пятиугольника меньше площади исходного, а дефект — больше (докажите это самостоятельно). Таким образом, можно построить бесконечную последовательность пятиугольников, площади которых убывают и становятся сколь угодно малыми (последнее утверждение требует доказательства и не является тривиальным, как кажется на первый взгляд!), а дефекты возрастают. Отсюда следует, что дефект любого пятиугольника отрицателен.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1987 | Убрать решения |