 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1988 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1988 |
|
|
a) Нужно вырезать из круга два маленьких равных кружка — один с центром в центре круга, а другой с центром в отмеченной точке, и затем поменять эти кружки местами.
б) Линия разреза — дуга того же радиуса, что и у данного круга, с центром в отмеченной точке (рис. 30).
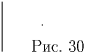
Задача 3: (5–9) Известно, что доля блондинов среди голубоглазых больше, чем доля блондинов среди всех людей. Что больше — доля голубоглазых среди блондинов или доля голубоглазых среди всех людей? Решение: Пусть L — количество всех людей, B — количество блондинов, G — количество голубоглазых, D — количество голубоглазых блондинов. Условие задачи означает выполнение неравенства
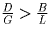 .
Умножим обе части этого неравенства на
.
Умножим обе части этого неравенства на 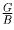 .
Получим
.
Получим
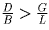 .
А это и значит, доля голубоглазых среди блондинов больше, чем доля
голубоглазых среди всех людей.
.
А это и значит, доля голубоглазых среди блондинов больше, чем доля
голубоглазых среди всех людей.Задача 4: (5–6) Можно ли нарисовать эту картинку (рис. 2), не отрывая карандаша от бумаги и проходя по каждой линии по одному разу?
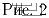
Нарисовать эту фигуру можно следующим образом. Пронумеруем три квадрата, из которых состоит фигура. Начнем рисовать первый квадрат с любой его точки до тех пор, пока не дойдем до точки пересечения со вторым квадратом. Затем прерываем обход первого квадрата и рисуем второй до тех пор, пока не дойдем до его точки пересечения с третьим. Затем рисуем полностью третий квадрат, окончив дорисовываем второй, затем — первый. Каждый раз мы будем оканчивать рисовать квадрат в той же точке, в которой начинали, то есть в точке пересечения с предыдущим квадратом.
Задача 5: (5–6) Прямая раскрашена в два цвета. Докажите, что на ней найдутся три точки A, B и C, окрашенные в один цвет такие, что точка B является серединой отрезка AC. Решение: Рассмотрим на прямой две произвольные точки X и Y, окрашенные в один цвет. Рассмотрим также три следующие точки: X1 — образ точки X относительно Y, Y1 — образ точки Y относительно X и O — середину отрезка XY (рис. 31). Если хотя бы одна из этих точек окрашена в тот же цвет, что и точки X и Y, то она вместе с ними образует искомую тройку. Если все эти три точки окрашены в другой цвет, то тогда они будут искомой тройкой. См. Т10.
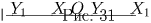
Фактически требуется доказать три неравенства
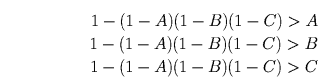
Докажем первое, остальные получаются из него переобозначениями.
Добавив к его обеим частям число A – (1 – A)(1 – B)(1 – C) > C, получаем
равносильное неравенство
1 – A > (1 – A)(1 – B)(1 – C).
Далее умножаем обе части на положительное число
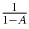 ,.
Имеем
1 > (1 – B)(1 – C).
Последнее неравенство справедливо, поскольку в его левой части
стоит произведение двух положительных чисел, меньших единицы. Из
этого следует справедливость исходного неравенства (см. Т13).
,.
Имеем
1 > (1 – B)(1 – C).
Последнее неравенство справедливо, поскольку в его левой части
стоит произведение двух положительных чисел, меньших единицы. Из
этого следует справедливость исходного неравенства (см. Т13).
Задача 7: (7–9) В треугольнике две высоты не меньше сторон, на которые они опущены. Найдите углы треугольника. Решение: Обозначим стороны треугольника a, b и c так, что высоты, опущенные на стороны a и b, не меньше этих сторон. Обозначим также ha, hb и hc высоты, опущенные на стороны a, b и c соответственно. По условию ha ≥ a, hb ≥ b. Кроме того, поскольку перпендикуляр является кратчайшим расстоянием от точки до прямой, ha ≤ b, hb ≤ a. Объединяя выписанные неравенства, получаем a ≤ ha ≤ b ≤ hb ≤ a, откуда очевидно a = b = ha = hb.
Условие a = b означает, что треугольник равнобедренный, а условия a = hb и b = ha что стороны a и b являются одновременно высотами, то есть они перпендикулярны друг другу. Итак, рассматриваемый треугольник прямоугольный и равнобедренный. Его углы 90, 45 и 45.
Задача 8: (7) На плоскости нарисовано некоторое количество равносторонних треугольников. Они не пересекаются, но могут иметь общие участки сторон. Мы хотим покрасить каждый треугольник в какой-нибудь цвет так, чтобы те из них, которые соприкасаются, были покрашены в разные цвета (треугольники, имеющие одну общую точку, могут быть покрашены в один цвет). Хватит ли для такой раскраски двух цветов? Решение: Будем называть два треугольника параллельными, если какая-то сторона одного из них параллельна какой-то стороне другого. Если два равносторонних треугольника, лежащих в одной плоскости, параллельны, то легко понять, что каждая сторона одного из них параллельна некоторой стороне другого. Поэтому параллельность на множестве равносторонних треугольников на плоскости является отношением эквивалентности (см. Т3).
Поскольку каждый треугольник может иметь общий участок стороны только с параллельным ему треугольником, то раскраску можно производить для каждого «класса параллельности" независимо. Покажем, как покрасить в два цвета, удовлетворяя условиям задачи, треугольники одного «класса параллельности". Введем для этого на «классе параллельности" понятие ориентации так, чтобы два треугольника на рис. 32,a) были одинаково ориентированными, а два треугольника на рис. 32,б) — противоположно ориентированными. Для того, чтобы дать строгое определение, отметим, что любые два параллельных треугольника гомотетичны (докажите это). Назовем два гомотетичных треугольника одинаково ориентированными, если коэффициент гомотетии положителен, и противоположно ориентированными, если он отрицателен. Таким образом, весь «класс параллельности" распадается на два подкласса так, что любые два треугольника одного подкласса одинаково ориентированы, а различных подклассов — противоположно ориентированы.
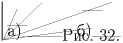
Очевидно, что два треугольника могут иметь общий участок сторон, только если они противоположно ориентированы. Поэтому если мы покрасим в один цвет все треугольники одной ориентации, а в другой цвет — все треугольники противоположной ориентации, то получим раскраску в два цвета, удовлетворяющую условию задачи.
Задача 9: (8–9) Доказать неравенство
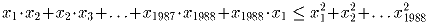
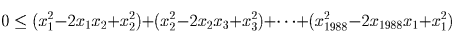
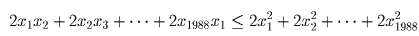
Задача 10: (8–9) В алфавите племени Мумбу-Юмбу есть лишь две буквы A и Б. Два разных слова обозначают одно и то же понятие, если одно из них может быть получено из другого с помощью следующих операций:
— в любом месте слова комбинацию букв АБА можно заменить на БАБ; — из любого места можно выкидывать две одинаковые буквы, идущие подряд.
Может ли дикарь племени сосчитать все пальцы на своей руке? А дни недели?
Решение:
Покажем, что в языке Мумбу-Юмбу может быть выражено не более шести понятий. Сначала докажем, что любое выражаемое понятие может быть выражено словом не более, чем из трех букв. Пусть мы имеем Мумбу-Юмбовское слово, состоящее не менее, чем из четырех букв. Покажем, как его сократить, чтобы смысл не изменился. Если в слове есть две одинаковые буквы, идущие подряд, то их нужно выкинуть. Если таких букв нет, то это значит, что в этом слове буквы чередуются. Значит, начало этого слова имеет вид либо АБАБ, либо БАБА. Начало АБАБ можно заменить на БАББ и далее на более короткое БА. Аналогично, БАБА заменяется на АБ. Таким образом, любое слово, состоящее не менее чем из четырех букв можно сократить, значит любое понятие можно выразить словом, состоящим не более чем из трех букв.
Перечислим теперь различные понятия языка Мумбу-Юмбу:
1) понятия, выражаемые словами из одной буквы: А, Б;
2) понятия, выражаемые словами из двух букв: АА, АБ, БА. Слова ББ и АА означают одно и то же, так оба они могут быть получены вычеркиванием пары одинаковых букв из слова ААББ.
3) понятия, выражаемые словами из трех букв: здесь имеем только одно новое понятие АБА. Действительно БАБ, по условию, означает то же самое, а в любых других трехбуквенных словах есть две одинаковые буквы, идущие подряд, поэтому они означают то же, что и уже перечисленные однобуквенные слова.
Итак, в языке Мумбу-Юмбу может быть выражено не более шести различных понятий. Поэтому дни недели дикарь племени посчитать не сможет.
Докажем теперь, что перечисленные слова языка Мумбу-Юмбу означают различные понятия. Для этого предположим, что дикарь, произнося любое слово, исполняет параллельно ритуальный танец следующим образом. На земле нарисован круг, разделенный на шесть равных секторов, один из которых отмечен. Обозначим три прямые, делящие круг, через a, b и c так, что выделенный сектор ограничен прямыми a и b. Дикарь становится сначала в отмеченный сектор и, произнося А, прыгает в сектор, симметричный тому, в котором он находится, относительно прямой a, а произнося Б — в сектор, симметричный относительно прямой b. Тогда если два слова означают одно и то же понятие, то в результате их произнесения, дикарь окажется в одном и том же секторе. Действительно, два прыжка через одну прямую оставят дикаря на месте, то есть выкидывание из слова двух одинаковых букв не повлияет на положение дикаря после танца. Комбинация букв АБА соответствует трем последовательным прыжкам через прямые a, b и снова a, что, нетрудно проверить, то же самое, что один прыжок через c. Тот же результат будет при последовательности прыжков, соответствующих комбинации БАБ. Поэтому замена АБА на БАБ тоже не влияет на место, в котором окажется дикарь после произнесения слова. Нетрудно проверить, что в результате произнесения слов А, Б, АА, АБ, БА и АБА дикарь окажется в различных секторах (см. рис. 33). Поэтому перечисленные шесть слов обозначают шесть различных понятий. Значит, для обозначения пальцев на руке понятий языка хватит.

| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1988 | Убрать решения |