Задача 1:
(5–6)
У Джона была полная корзина тремпончиков. Сначала он
встретил Анну и дал ей половину своих тремпончиков и еще
пол-тремпончика. Потом он встретил Банну и отдал ей половину
оставшихся тремпончиков и еще пол-тремпончика. После того, как
он встретил Ванну и снова отдал ей половину тремпончиков и еще
пол-тремпончика, корзина опустела. Сколько тремпончиков было у
Джона вначале? Что такое тремпончики выяснить не удалось, так как
к концу задачи их не осталось.
Задача 2:
(5–9)
На турнире им. Ломоносова 19лохматого года в институте
МИМИНО были конкурсы по математике, физике, химии, биологии и
бальным танцам. Когда турнир закончился, выяснилось, что на
каждом конкурсе побывало нечетное количество школьников, и каждый
школьник участвовал в нечетном количестве конкурсов. Четное или
нечетное число школьников пришло на турнир в МИМИНО?
Задача 3:
(5–7)
Один из пяти братьев испек маме пирог. Андрей сказал:
«Это Витя или Толя". Витя сказал: «Это сделал не я и не Юра".
Толя сказал: «Вы оба шутите". Дима сказал: «Нет, один из них
сказал правду, а другой — нет". Юра сказал: «Нет Дима, ты не
прав". Мама знает, что трое из ее сыновей всегда говорят правду.
Кто испек пирог?
Задача 4:
(5–7)
Даны две окружности и точка. Построить отрезок, концы
которого лежат на данных окружностях, а середина — в данной
точке.
Задача 5:
(8–9)
На конкурсе по математике в институте МИМИНО предлагалось
20 задач. На закрытие пришло 20 школьников. Каждый из них решил
по две задачи, причем выяснилось, что среди пришедших каждую
задачу решило ровно два школьника. Докажите, что можно так
организовать разбор задач, чтобы каждый школьник рассказал одну
из решенных им задач, и все задачи были разобраны.
Задача 6:
(8–9)
По окончании конкурса бальных танцев, в котором
участвовали 7 мальчиков и 8 девочек, каждый (каждая) назвал
(назвала) количество своих партнерш (партнеров): 3, 3, 3, 3, 3,
5, 6, 6, 6, 6, 6, 6, 6, 6, 6. Не ошибся ли кто-нибудь из них?
Задача 7:
(8–9)
Одно из чисел получается из другого перестановкой цифр.
Может ли их сумма равняться 999…9 (999 девяток)?
Задача 8:
(8–9)
Восстановите а) треугольник; б) пятиугольник по серединам его
сторон.
Задача 9:
(8–9)
Первоклассник Петя знает только цифру 1. Докажите, что он
может написать число, делящееся на 1989.
Задача 10:
(8–9)
Каков наибольший возможный общий делитель чисел 9m + 7n и
3m + 2n, если числа m и n не имеют общих делителей, кроме единицы?
Задача 11:
(8–9)
Барон Мюнхгаузен заявил Георгу Кантору, что он может
выписать в ряд все натуральные числа без единицы так, что только
конечное их число будет больше своего номера. Не хвастает ли
барон?
Задача 12:
(8–9)
Три окружности попарно пересекаются. Для каждой
пары окружностей через точки их пересечения проведена прямая.
Докажите, что эти три прямые либо попарно параллельны, либо
пересекаются в одной точке.
Задача 13:
(6–8)
Найдите все простые числа, которые нельзя записать в виде
суммы двух составных.
Задача 14:
(6–8)
Решить уравнение в целых положительных числах
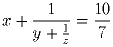
Задача 15:
(8)
Пусть a, b, c — длины сторон треугольника; α ,
β , γ — величины противолежащих углов. Докажите,
что
a α + b β + c γ ≥ a β + b γ + c α .