 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1990 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1990 |
|
|
Задача 2: (7–8) Из квадратного листа бумаги в клетку, содержащего целое число клеток, вырезали квадрат, содержащий целое число клеток так, что осталось 124 клетки. Сколько клеток мог содержать первоначальный лист бумаги? Решение: Задача сводится к решению в целых положительных числах уравнения x² – y² = 124, которое можно переписать в виде (x – y)(x + y) = 124. Пусть (x,y) — решение этого уравнения. Предположим, x и y имеют разную четность (то есть одно из них нечетно, а другое — четно). Тогда числа x – y и x + y — оба нечетные, значит, их произведение нечетно и не может быть равно 124. Поэтому x и y имеют одинаковую четность (то есть либо оба нечетные, либо оба четные), значит числа x + y и x – y четные. Единственный способ разложить число 124 на два четных сомножителя — это 2 • 62. Значит сумма чисел x и y равна 62, а разность — 2. Откуда x = 32, y = 30. Первоначальный лист бумаги содержал 32² = 1024 клетки. (См. также Т9.)
Задача 3: (7–8) Можно ли на плоскости нарисовать 12 окружностей так, чтобы каждая касалась ровно пяти окружностей? Решение: Требуемое расположение показано на рис. 38.

Задача 4: (7–8) В таблице 10 × 10 по порядку расставлены числа от 0 до 99 (в первой строке — от 0 до 9, во второй строке — от 10 до 19 и т.д.). Затем перед каждым из чисел поставлен знак « + " или « – " так, что в каждой строке и каждом столбце оказалось по пять знаков « + " и пять знаков « – ". Чему может быть равна сумма всех чисел таблицы с учетом расставленных знаков? Решение: Представим данную таблицу в виде суммы двух таблиц, разбив каждый ее элемент на десятки и единицы (рис. 39).

Задача 5: (9–10) Дан куб 4 × 4 × 4. Расставьте в нем 16 ладей так, чтобы они не били друг друга. Решение:
Решение аналогично решению задачи 87.13. На рис. 40 требуемое расположение ладей приведено явно.
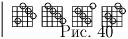
Задача 6: (9–10) Вершины правильного треугольника находятся на сторонах AB, CD и EF правильного шестиугольника ABCDEF. Докажите, что они имеют общий центр. Решение:
Пусть XYZ — данный треугольник, KLM — треугольник, получаемый при продолжении сторон AB, CD и EF шестиугольника ABCDEF (рис. 41). Пусть O — центр треугольника XYZ, докажем, что он является центром треугольника KLM.
При повороте относительно точки O на 120 против часовой стрелки прямая AB переходит в прямую, параллельную CD. Поскольку при этом повороте точка X прямой AB переходит в точку Y, то образ прямой AB должен проходить через точку Y, значит совпадать с CD. Поэтому точка O равноудалена от прямых AB и CD. Аналогично доказывается, что она равноудалена от прямых CD и EF. Значит, она является центром окружности, вписанной в треугольник KLM и, тем самым, центром шестиугольника ABCDEF.
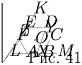
Задача 7: (9–10) Произведение двух положительных чисел больше их суммы. Докажите, что эта сумма больше четырех. Решение: Пусть x и y — данные числа. Условие x + y < xy можно переписать в виде (x – 1)(y – 1) > 1, откуда очевидно, что x > 1, y > 1. Неравенство о среднем арифметическом и среднем геометрическом (см. Т13) для положительных чисел x – 1 и y – 1 дает
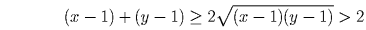
Задача 8: (9–10) В булке за 10 копеек оказался запечен изюм двух сортов. Докажите, что внутри булки найдутся две такие точки, удаленные на расстояние 1,см, что они либо не принадлежат никаким из изюмин, либо принадлежат изюминам одного сорта.
Решение: Рассмотрим правильный тетраэдр с ребром 1,см, расположенный целиком внутри булки. Для каждой из его вершин существует одна из трех возможностей — либо находиться внутри изюмины одного из двух сортов, либо не принадлежать никакой изюмине. Поскольку всего вершин четыре, а возможностей — три, то для каких-то двух вершин выполнена одна и та же возможность (см. Т2). Эти две вершины и будут искомыми точками. См. Т10.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1990 | Убрать решения |