Задача 1:
(7–8)
На плоскости отмечены четыре точки. Докажите, что их
можно разбить на две группы так, что эти группы точек нельзя
будет отделить одну от другой никакой прямой.
Задача 2:
(7–8)
На шахматной доске 4 × 4 расположена
фигура — «летучая ладья", которая ходит так же, как обычная
ладья, но не может за один ход стать на поле, соседнее с
предыдущим. Может ли она за 16 ходов обойти всю доску, становясь
на каждое поле по разу, и вернуться на исходное поле?
Задача 3:
(7–8)
Докажите, что
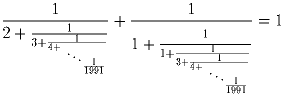
Задача 4:
(7–8)
По окружности стоит 6 чисел; каждое равно модулю разности
двух чисел, стоящих после него по часовой стрелке. Сумма всех
чисел равна 1.
a) Найдите набор чисел, удовлетворяющий данному условию.
б) Сколько различных таких наборов существует? Решения,
получающиеся друг из друга поворотом окружности, считаются
одинаковыми.
Задача 5:
(9–10)
Через центр окружности ω
1 проведена окружность ω
2;
A и B — точки пересечения окружностей. Касательная к
окружности ω
2 в точке B пересекает окружность ω
1
в точке C. Докажите, что AB = BC.
Задача 6:
(9–10)
В лес пошло 11 девочек и n мальчиков. Вместе они собрали
n² + 9n – 2 гриба, причем все они собрали поровну грибов. Кого было
больше: мальчиков или девочек?
Задача 7:
(9–10)
В треугольнике ABC на стороне AB выбрана точка D
такая, что
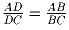
,.
Докажите, что угол C — тупой.
Задача 8:
(9–10)
Шеренга солдат называется неправильной, если никакие три
подряд стоящих солдата не стоят по росту (ни в порядке
возрастания, ни в порядке убывания). Сколько неправильных шеренг
можно построить из n солдат разного роста, если
а) n=4;
б) n=5?


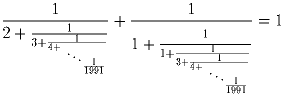
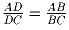 ,.
Докажите, что угол C — тупой.
Задача 8:
(9–10)
Шеренга солдат называется неправильной, если никакие три
подряд стоящих солдата не стоят по росту (ни в порядке
возрастания, ни в порядке убывания). Сколько неправильных шеренг
можно построить из n солдат разного роста, если
,.
Докажите, что угол C — тупой.
Задача 8:
(9–10)
Шеренга солдат называется неправильной, если никакие три
подряд стоящих солдата не стоят по росту (ни в порядке
возрастания, ни в порядке убывания). Сколько неправильных шеренг
можно построить из n солдат разного роста, если