 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1991 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1991 |
|
|
1) Все четыре точки лежат на одной прямой. Обозначим их A, B, C и D в порядке. в котором они расположены на прямой. Тогда в первую группу следует поместить точки A и C, а во вторую — B и D.
2) Только три из четырех точек лежат на одной прямой. Обозначим их A, B и C в порядке, в котором они расположены на прямой, четвертую точку обозначим D. В этом случае опять помещаем точки A и C в первую группу, а B и D — во вторую.
3) Точки являются вершинами выпуклого четырехугольника. Тогда в первую группу следует отнести концы одной его диагонали, а во вторую — концы другой диагонали.
4) Одна из этих точек лежит внутри треугольника с вершинами в трех других точках. В этом случае эта одна точка образует первую группу, а три остальные точки — вторую.
Задача 2: (7–8) На шахматной доске 4 × 4 расположена фигура — «летучая ладья", которая ходит так же, как обычная ладья, но не может за один ход стать на поле, соседнее с предыдущим. Может ли она за 16 ходов обойти всю доску, становясь на каждое поле по разу, и вернуться на исходное поле?
Решение: На рис. 42 поля шахматной доски 4 × 4 пронумерованы в порядке, в котором «летучая ладья" может обойти их, соблюдая условия задачи.
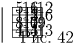
Задача 3: (7–8) Докажите, что
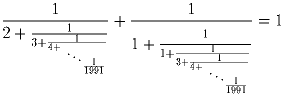
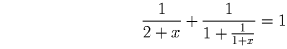
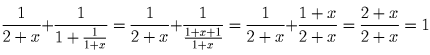
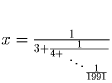
Задача 4: (7–8) По окружности стоит 6 чисел; каждое равно модулю разности двух чисел, стоящих после него по часовой стрелке. Сумма всех чисел равна 1.
a) Найдите набор чисел, удовлетворяющий данному условию.
б) Сколько различных таких наборов существует? Решения, получающиеся друг из друга поворотом окружности, считаются одинаковыми.
Решение: Поскольку каждое из выписанных чисел равно модулю разности двух других, а модуль любой величины всегда неотрицателен, то все числа должны быть неотрицательны. Пусть наибольшее из них равно x. Два следующих за ним числа должны быть не больше x и различаться на x. Это возможно лишь в случае, когда одно из них равно x, а другое — нулю. Итак, в каком-то месте должны стоять либо числа x, x, 0, либо числа x, 0, x. Двигаясь по окружности против часовой стрелки, мы однозначно восстановим остальные числа. В обоих случаях получается один и тот же набор — x, x, 0, x, x, 0. Из условия, что сумма всех чисел равна 1, находим x = ¼.Задача 5: (9–10) Через центр окружности ω 1 проведена окружность ω 2; A и B — точки пересечения окружностей. Касательная к окружности ω 2 в точке B пересекает окружность ω 1 в точке C. Докажите, что AB = BC. Решение: Пусть O — центр окружности ω 1 (рис. 43). Тогда в силу симметрии дуги AO и OB окружности ω 2 равны. Кроме того, угол OBC равен половине дуги OB, как угол между касательной и хордой, а угол OBA равен половине дуги OA, как вписанный (см. Т18). Поэтому углы OBC и OBA равны, и прямые BC и BA симметричны относительно радиуса OB окружности ω 1. Значит, при этой симметрии их точки A и C пересечения с окружностью ω 1 переходят друг в друга. Отсюда следует, что AB = BC.
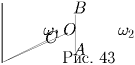
Задача 6: (9–10) В лес пошло 11 девочек и n мальчиков. Вместе они собрали n² + 9n – 2 гриба, причем все они собрали поровну грибов. Кого было больше: мальчиков или девочек? Решение: Из условия задачи следует, что n² + 9n – 2 делится на n + 11. Значит, на n + 11 делится также (n² + 9n – 2) – (n – 2)(n + 11) = 20, откуда следует, что n + 11 ≤ 20, значит n ≤ 9. Мы получили, что мальчиков было не больше девяти. Значит, их было меньше, чем девочек.
Задача 7: (9–10) В треугольнике ABC на стороне AB выбрана точка D такая, что
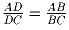 ,.
Докажите, что угол C — тупой.
Решение:
Теорема синусов (см. Т19), примененная к треугольникам
ABC и ADC, дает
,.
Докажите, что угол C — тупой.
Решение:
Теорема синусов (см. Т19), примененная к треугольникам
ABC и ADC, дает
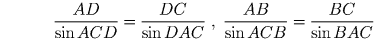
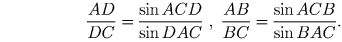
Учитывая условие задачи и то, что углы DAC и BAC равны, получаем sin ACD = sin ACB. Так как углы ACB и ACD не равны, то последнее равенство означает, что их сумма равна 180. Значит, больший из них — угол ACB — тупой.
Задача 8: (9–10) Шеренга солдат называется неправильной, если никакие три подряд стоящих солдата не стоят по росту (ни в порядке возрастания, ни в порядке убывания). Сколько неправильных шеренг можно построить из n солдат разного роста, если
а) n=4;
б) n=5?
Решение: Рассмотрим самого высокого солдата в некоторой неправильной шеренге. Докажем, что после него могут стоять не более двух солдат. Для этого предположим противное, что после него стоят по крайней мере трое. Если они стоят по росту в порядке возрастания, то это противоречит условию неправильности шеренги. Если же какие-то двое из них стоят в порядке убывания, то они вместе с самым высоким солдатом образуют тройку стоящих по росту солдат, что опять противоречит условию неправильности шеренги. Полученное в обоих случаях противоречие доказывает сформулированное утверждение. Аналогичные рассуждения показывают, что и перед самым высоким солдатом в неправильной шеренге могут стоять не более двух солдат, и что то же самое верно для самого низкого солдата.
а) Обозначим солдат буквами A, B, C и D (по росту). Приведенное выше рассуждение показывает, что в неправильной шеренге солдаты A и D должны стоять в середине, а солдаты B и C, тем самым, по краям. Таким образом, мы можем получить 4 неправильных шеренги: BADC, BDAC, CADB и CDAB.
б) Из приведенного выше рассуждения следует, что в неправильной шеренге из пяти солдат самый высокий должен стоять посередине (на третьем месте), то же самое можно утверждать и про самого низкого. Значит, неправильной шеренги из пяти солдат построить нельзя.
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1991 | Убрать решения |