 |
 |
|
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1994 | Убрать решения |
|
|
| Турнир имени Ломоносова. Конкурс по математике. 1994 |
|
|
Решение:
Пусть на балу присутствовали три девушки — Анна, Вера и Светлана. Пусть также по красоте девушки расположены в порядке: Светлана–Анна–Вера (Вера — самая красивая), а по уму — в порядке Вера–Светлана–Анна (Анна — самая умная). Предположим, что каждый юноша, танцевавший с Анной, приглашает на следующий танец с Веру (более красивую девушку), танцевавший с Верой — Светлану, (более умную), танцевавший со Светланой — Анну (одновременно более красивую и более умную). Как видим, описанная в задаче ситуация могла быть.
Задача 2: (7–9) На плоскости даны 2 окружности, одна внутри другой. Циркулем и линейкой построить такую точку O, что внешняя окружность получается из внутренней растяжением с центром в точке O. («Растяжение (или гомотетия с положительным коэффициентом) с центром в точке O" означает преобразование плоскости, оставляющее точку O и все проходящие через нее прямые на месте и изменяющее все расстояния в одно и то же число раз.) Решение:
Пусть O — искомая точка, A1 и B1 — две диаметрально противоположные точки внутренней окружности, A2 и B2 — соответствующие точки внешней окружности. Согласно определению гомотетии, треугольники OA1B1 и OA2B2 подобны (по трем сторонам). Значит, ∠ OA1B1 = ∠ OA2B2, и прямые A1B1 и A2B2 параллельны.
Отсюда следует искомое построение: через центры O1 и O2 окружностей ω 1 и ω 2 проводим параллельные (но не совпадающие) прямые l1 и l2; точки пересечения прямой l1 с окружностью ω 1 обозначаются A1 и B1, а прямой l2 с окружностью ω 2 — A2 и B2 (так, что точки A1 и A2 лежат по одну сторону от прямой O1O2). Точка пересечения прямых A1A2 и B1B2 и будет искомой точкой O (рис. 45).
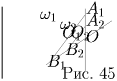
Задача 3: (7–9) В Простоквашинской начальной школе учится всего 20 детей. У любых двух из них есть общий дед. Докажите, что у одного из дедов в этой школе учится не менее 14 внуков и внучек.
Решение:
Докажем сначала, что у учеников Простоквашинской начальной школы либо есть не более трех различных дедов, либо один дед является общим для всех детей. Представим ситуацию графически. Обозначим дедов точками на плоскости, соединив две точки отрезками, если соответствующие деды имеют общих внуков (хотя-бы одного). Тогда по условию задачи, любые два нарисованных отрезка имеют общий конец. Рассмотрим два таких отрезка (если двух различных отрезков не существует, то все дети являются общими внуками двух дедов). Пусть это будут отрезки AB и AC. Тогда любой другой отрезок должен иметь либо конец в вершине A, либо два конца в вершинах B и C. При этом, если отрезок BC проведен, то никаких других отрезков, кроме AB, AC и BC быть не может.
Итак, граф имеет один из двух видов, приведенных на рис. 46. Первый из них соответствует случаю, когда все дети имеют общего деда, тем самым, у этого деда имеется 20 внуков среди учеников школы. Рассмотрим второй случай. Предположим, что дедов зовут Иван, Петр и Степан. Тогда все дети являются общими внуками, либо Ивана и Петра, либо Ивана и Степана, либо Петра и Степана. По крайней мере у одной из этих пар (скажем, Степана и Петра) количество общих внуков не превосходит 6. Действительно, если бы у всех трех пар количество общих внуков было не меньше 7, то всего детей было бы не меньше 21, что противоречит условию (приведенное рассуждение фактически следует принципу Дирихле (см. Т2), хотя и в слегка модернизированном виде). Но тогда все остальные дети (а их не меньше 20 – 6 = 14) являются внуками Ивана.
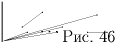
| Задачная база >> Московские соревнования >> Турнир имени Ломоносова >> 1994 | Убрать решения |